Тема "Прямоугольная система координат"
Цель урока —  научить учащихся строить точки по заданным её координатам и определять координаты точки, отмеченной на координатной плоскости;
Задачи урока:

• ознакомить учащихся с прямоугольной системой координат на плоскости;
• научить  свободно ориентироваться на координатной плоскости, хорошо воспринимать на слух координаты; четко и аккуратно выполнять геометрические построения;
• развивать творческие способности;
• воспитывать интерес к предмету и ответственность за общий результат

Тип урока — комбинированный (изучение нового материала, практикум, систематизация знаний и умений)
Форма урока — урок-игра
Оборудование — Компьютер, слайды.
В качестве учебного пособия используется учебник математики 6 класса авт. Алдамуратова Т.А.
Ход урока
1.    Организационный момент
2.    Объяснение нового материала
Мотивационный материал
— Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего? …Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы. Суть координат или системы координат состоит в том, что это правило, по которому определяется положение объекта.
Системы координат окружают нас повсюду  

• чтобы правильно занять свое место в кинотеатре нужно знать две       координаты — ряд и место;
• система географических координат (широта — параллели и долгота — меридианы);
• те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами — буквой и цифрой:
• с помощью координатной сетки летчики, моряки определяют местоположение объектов;
• применяются на туристических схемах для поиска достопримечательности или нужной улицы;
• при астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре.

Исторический материал   — Как давно системы координат пронизывают практическую жизнь человека?
Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.    Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат. Но эти понятия впервые были систематизированы в 17 веке Рене Декартом. Рене Декарт (1596-1650) — французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.
Координатная плоскость
При изучении темы «Координатная прямая», мы научились находить по координате положение точки на прямой. А как указать положение точки на плоскости? Для этого нам понадобиться координатная плоскость. Рассмотрим ее составляющие:

• две перпендикулярные прямые — оси координат (часто называют  — прямоугольная система координат)
• вертикальная — ось абсцисса (х), горизонтальная — ось ордината (у), стрелки осей указывают положительные направления,
• начало координат —  точка пересечения прямых,
• на  прямых,  вводят обычные координаты, которые согласованы между собой

Нахождение координат точек. Построение точек на плоскости по заданным координатам.

Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса (х) и ордината (у). И наоборот, каждой паре чисел (х; у) соответствует единственная точка на плоскости. Координаты точки записывают в скобках через точку с запятой, причем первой всегда записывается координата х, второй координата у.
3.      Актуализация опорных знаний
Предлагаю вам сейчас применить изученный материал на практике. Для этого выполним ряд практических заданий:

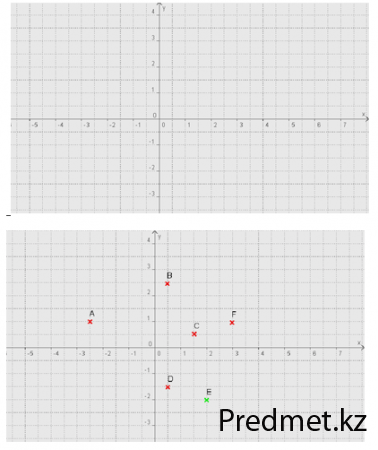
• определите координаты точек  A, B, C, D, E, F;
• укажите место точек на координатной плоскости Н(1;4), Т(-2;5),  К(-3;-4),Е(5;-2), О(0;0).
• Определить координаты зарытых кладов и получите сокровище капитана Флинта.   
• Дневник в студию.
• Тебе не повезло дружок.

4.      Закрепление изученного материала
Задание: На нашем острове обитает много животных, в океане плавают рыбы. Нарисуйте их по данным координатам, придумайте им свои названия (задание выполняется в рабочих тетрадях).
Школа Робинзона Крузо.  

• Домашнее задание §35 №1125, №1128.
• Итог урока.

Объявляются оценки за урок.
Ребята выбирают и говорят свою оценку урока.
Скачать урок [attachment=243]

Урок математики по теме \»Прямоугольная система координат\».

6-й класс

Данный урок построен по проектной методике. Чрезвычайно важно показать детям их личную заинтересованность в приобретаемых знаниях, которые могут и должны пригодиться им в жизни.

В основе метода проектов лежит развитие познавательных навыков учащихся, умений самостоятельно конструировать свои знания, умений ориентироваться в информационном пространстве, развитие критического и творческого мышления.

Использование мультимедийные средств обучения делает учебный проект более привлекательным, рациональным, способствует формированию устойчивого интереса к предмету.

Цель урока: Обобщение понятий, связанных с координатной плоскостью и координатами точек на плоскости; закрепление алгоритмов нахождения координат точки на плоскости и отыскания точки по ее координатам.

Оборудование:

Обучающий аспект

• Расширить понятие координатной плоскости;
• Продолжить формирование умений нахождения точки по заданным координатам и координат данного объекта, формирование навыков графической культуры;
• Интегрирование знаний различных дисциплин (география, традиции, литература);
• Приобретение навыков использования обучающих мультимедийные продуктов.

Развивающий аспект

• Развитие умений сравнивать, классифицировать, выделять главное в изучаемом объекте, адаптировать полученные знания к практике;
• Развитие таких качеств, как потребность в приобретении новых знаний, овладение способами познавательной деятельности.

Самообразовательный аспект

• Обеспечить развитие у школьников умения ставить цель и планировать свою деятельность;
• Создать условия для развития умения работать во времени;
• Приобретение навыков самостоятельного, творческого поиска ответов на основе имеющегося опыта с одновременным обогащением его, а также последующего поиска истины;
• Содействовать развитию у детей умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.

Стимулирующий аспект

• Формирование устойчивого интереса к предмету, побуждение учащихся к дальнейшему познанию, используя следующие средства обучения:
• компьютерную презентацию;
• мультимедийные средства обучения;
• видеосюжет;
• Интернет.

Средства обучения

• Компьютер, проектор, экран;
• Рабочие листы.

Программные средства и цифровые ресурсы

• Программы Microsoft Word, Microsoft Power Point.
• Интернет-ресурсы

 

Ход урока

I. Организационный момент. Сообщение темы и целей урока.

Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости. Поздоровайтесь с ними. Садитесь. Тема нашего урока «Прямоугольна система координат. Построение точки по ее координатам (слайд 1). Сегодня на уроке мы:

1. Обобщим понятия, связанные с координатной плоскостью и координатами точки на плоскости.
2. Закрепим алгоритмы отыскания точки по ее координатам и нахождения координат точки на координатной плоскости (слайд 2).

II. Объяснение новой темы.

Рассказ учителя:

«Координата» слово греческого происхождения, означает место нахождения кого-либо.

Идея координат зародилась в древности.

Первоначальное их применение связано с астрономией и географией, то есть, с потребностью определять положение светил на небе и определенных объектов на поверхности земли. Следы применения координат были обнаружены еще в Древнем Египте на стенах погребальных камер (показ слайда),

 

 а так же в работах художников эпохи Возрождения (показ слайда).

 

 

— Нам известно, что такое координатная прямая.  Проведем две взаимно перпендикулярных координатных прямых. Точку  их пересечения отметим через О.   Они образуют прямоугольную систему координат.  (слайд)

 

Они имеют общее начало отсчета и одинаковые единичные отрезки.

 Прямоугольная система координат названа декартовой координатной системой координат в честь фрацузского философа и математика Рене Декарта (1596-1650).

 

Именно его имя носит прямоугольная система координат.

 

 

Координатные прямые называются координатными осями. 

Горизонтальная координатная прямая называется ось. абцисс (Ох) и обозначается буквой х.

Вертикальная прямая называется осью ординат (Оу) и обозначается буквой у.

Точка пересечения оси абцисс с осью ординат называется началом координат. Обозначается буквой О, потому что буква О- первая буква латинского алфавита, которое означает «начало».

Чтобы найти координаты точки М на координатной плоскости, надо:

1) из точки М провести перпендикуляр на ось абцисс. Найти координату точки пересечения этого перпендикуляра с осью Ох. Она и является абциссой точки М;

2) из точки М провести перпендикуляр на ось ординат. Найти координату точки пересечения этого перпендикуляра с осью Оу. Она и является ординатой точки М.

На рисунке абцисса точки М равна 3; ордината ее равна 5.

Абцисса и ордината заданной точки называются координатами точки.

Читают: «Точка М с координатами 3 и 5».

При записи координат точки абцисса записывается на первом месте, а ордината – на втором месте.

Место точки на плоскости определяется парой чисел.

 

Если точка лежит на оси абцисс (Ох), то ее ордината равно 0. Например, С (6; 0); К (-4; 0).

 

 

 

 

Если точка лежит на оси ординат (Оу), то ее абцисса равна 0. например, В(0;3);  F (0; -6).

 

Построение точки по ее координатам.

Построим на координатной плоскости точку А (4;3).

Для этого надо:

1) на оси абцисс (Ох) отметить точку, имеющую координаты х = 4, у= 0 и провести  через нее прямую , перпендикулярную на абцисс (Ох).

2) на оси ординат (Оу) отметить точку, имеющую  координаты х=0; у=3 и провести через нее прямую, перпендикулярную оси ординат (Оу).

3) точка пересечения перпендикуляров А- искомая точка А (4; 3).

 

 

 Задание.

Построить  на координатной плоскости следующие точки:

М(4;3)       К(-4;3)      А(-4;-3)                   В (4; -3)

Полученные точки находятся на разных частях плоскости.

Они называются координатными четвертями.

Порядковые номера координатных четвертей

определяются против часовой стрелки.

I   II  III  IV

 

Рассказ учителя, сопровождающийся слайдами:

Системы координат с двумя величинами называют двухмерными, а с тремя – трехмерными, есть и пространства с числом измерений больше трех.

1. прямоугольная система координат в трех мерном

 

2. полярная система координат;

 

3. цилиндрическая систем координат;

 

4. косоугольная система координат;

 

5. сферическая система координат.

 

 

III,  Выполнение заданий.

— Итак, есть желание самим построить точки? Тогда постройте точки в координатной плоскости и соедините их в соответствующем порядке.

Учащиеся работают в группах по карточкам:

№ 1

а) (2; 6), (5; 6), (2; 3), (3; 3), (2; 0),

б) (-6; 6), (-3; 6), (-6; 3), (-3; 3), (6; 0).

В результате получается число 33.

— Что это за дата? (номер нашей школы).

 

№ 2

а) (-6;-2), (-3;-2), (-3;-5), (-6;-8), (-3; -8),

б)  (2; -2), (5; -2), (5; -8), (2; -8),

В результате получается число 20.

— Что ассоциирует это число, как вы думаете? (недавно мы праздновали 20-лети независимости Казахстана).

Работа с учебником.

Стр.279. №1124 (1-3)

 

Стр.279. №1126

 

IV. Проверь себя

Задание: вставьте пропущенные слова, используя подсказки внизу текста

1)       Положение точки на плоскости можно задать ……….. числами.

2)       Проведём две ……….. координатные прямые, пересекающиеся в …….. их отсчёта.

3)       Горизонтальную координатную прямую называют осью …….. и обозначают буквой …., а вертикальную координатную прямую называют осью …….. и обозначают буквой …..

4)       Плоскость, на которой задана прямоугольная система координат, называют ………… плоскостью.

5)       Первую координату точки называют …., а вторую координату точки называют …………

6)       Оси координат разбивают плоскость на …. части. Нумерация четвертей происходит …………. движения часовой стрелки.

7)       Идея использования координат принадлежит ………… математику ………..

ПОДСКАЗКА:

Двумя,           начале,          французскому,                                            ординат,

абциссой,                  4,         Рене Декарт,                        Ох,                  координатной, 

Оу,                  против,          перпендикулярные,           абцисс,           ординатой.

Проверка проходит в быстром темпе – без права исправления. Учащиеся только фиксируют ошибки, а устранять их будут дома.

 

IV. Домашнее задание.

Стр. 279. № 1125, № 1136.

V. Итог урока.

1. Вспомните название темы урока?
2. Какая цель стояла перед вами на уроке?
3. Чему новому вы научились на уроке?
4. Какие ранее полученные знания вы использовали на уроке?
5. В какой новой ситуации вы применили свои знания на этом уроке?
6. Выскажите свое отношение к уроку.

VI. Подведение итогов. Выставление оценок.

 

Мусина Адемы Заманбековна,

учитель математики и информатики,

ГУ «СОШ №33 им.К.Рыскулбекова»

г.Семей