Исследовательская работа
МАГИЧЕСКИЕ КВАДРАТЫ

Высшее назначение математики – находить
порядок в хаосе, который нас окружает.
Норберт Винер
Великие ученые древности считали количественные отношения основой сущности мира. Поэтому числа и их соотношения занимали величайшие умы человечества. «В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты»- писал Бенджамин Франклин. Магический квадрат- это квадрат, сумма чисел которого в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из диагоналей одна и та же.
Некоторые выдающиеся математики посвятили свои работы магическим квадратам и полученные ими результаты оказали влияние на развитие групп, структур, латинских квадратов, определителей, разбиений, матриц, сравнений и других нетривиальных разделов математики.
Цель настоящей работы – знакомство с различными магическими квадратами и изучение областей их применения.
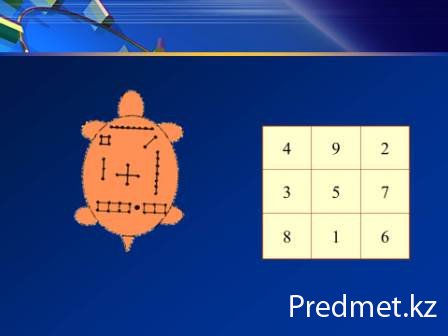
Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Первые упоминания о магических квадратах были у древних китайцев. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1. Подсчитав количество кружков каждой из фигур, получим магический квадрат 3*3.

Рис. 1
Изображение магического квадрата в виде связанныхкружков встречаются в более позднем трактате мыслителя Чжу Си. Вот как это эффектно он выглядел там.
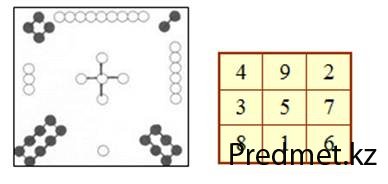
Черные кружки – это четные (женственные) числа, белые – нечетные (мужественные) числа.
В древнеиндийских надписях и трактатах встречаются изображения магических квадратов четвёртого порядка.
Из Индии сведения о магических квадратах перешли к арабам. Арабы были знакомы с квадратом третьего порядка в VIII веке, а в ХII веке его описал в своих сочинениях Ибн Эзра, испанский еврей, принявший мусульманство. Мусульмане очень благовейно относились к квадратам пятого порядка с цифрой 1 в середине, считая это изображение символом единства Аллаха. В Европе о магических квадратах узнали благодаря византийскому писателю Э. Мосхопулосу, жившему в Константинополе в начале XV века.
Редкостью является использование магического квадрата в изобразительном искусстве, а не в литературном или научном произведении. Впервые это сделал немецкий художник Альбрехт Дюрер (1471 – 1528), выпустивший в 1514 году гравюру «Меланхолия», на которой есть изображение магического квадрата четвёртого порядка. Причем два числа в середине нижней строки указывают на год создания гравюры – 1514.Этот факт говорит об умении в то время составлять магические квадраты с определённым заданным расположением некоторых чисел. Говорят, что гравюра А.Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса (1503-1566).

Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2х2 не существует. Существует единственный магический квадрат 3*3, так как остальные магические квадраты 3*3 получаются из него либо перестановкой строк (рис. 4а) или столбцов (рис. 4б) либо путем поворота исходного квадрата на 900 (рис. 4в) или на 1800 (рис 4г).
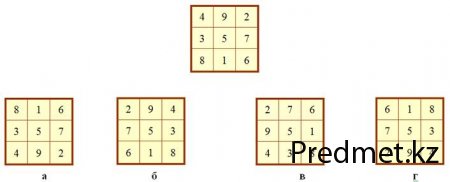
Рис. 4
В магическом квадрате 3х3 магической постоянной 15 должны быть равны сумме трех чисел по восьми направлениям: по 3 строкам, 3 столбца и 2 диагоналям.
Такой магический квадрат был у древних китайцев символом огромного значения. Цифра 5 в середине означала землю, а вокруг неё в строгом равновесии располагались огонь (2 и 7), вода (1 и 6), дерево (3 и 8), металл(4 и 9).
С увеличением размеров квадрата (числа клеток) быстро растёт количество возможных магических квадратов такого размера. Существует 880 магических квадратов порядка 4 и 275 305 224 магических квадратов порядка 5. Причем, квадраты 5х5 были известны ещё в середине века.
Квадраты нечетного порядка.
Требуется, положим, «смонтировать» хотя бы по одному магическому квадрату всевозможных нечетных порядков. Это можно сделать по единой схеме, а схем придумано много. Вот и воспользуемся одной из них для составления, например, квадрата пятого порядка, после чего эту схему без труда можно применить к квадратам третьего, седьмого и других нечетных порядков.
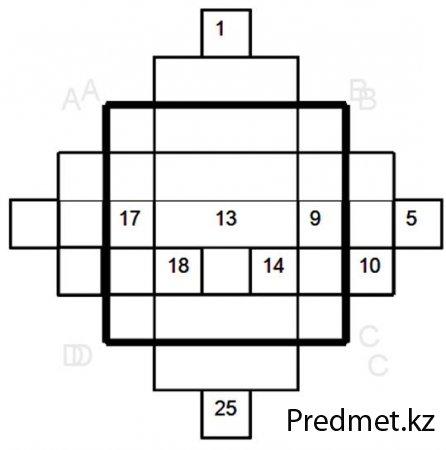
Строим квадрат ABCD (см. рисунок а на следующей странице) с 25 клетками и временно дополняем его до симметричной ступенчатой фигуры (изображенной на том же рисунке) со ступеньками в одну клетку. В полученной фигуре располагаем по порядку косыми рядами сверху — вниз — направо 25 целых чисел от 1 до 25. А теперь каждое число, оказавшееся вне квадрата ABCD, следует перенести вдоль того же ряда или столбца ровно на столько клеток от той клетки, которую оно занимает, каков порядок квадрата, в вашем примере — на пять. Так, в соответствии с этим правилом, число 6 надо поместить в клетку под числом 18, а число 24 — выше числа 12, далее, 1 — ниже 13, а 25 — выше 13; 16 — правее 8, а 4 — левее 12 и т. д.
Получится магический квадрат, изображенный на рисунке б на следующей странице.
Нетрудно убедиться в том, что в получившемся квадрате выполняются основные свойства, магического квадpaтa, тех есть сумма чисел вдоль каждой диагонали, вдоль каждой горизонтали и вертикали одна и та же и равна 65. Это число называется константой квадрата пятого порядка. Но у получившегося квадрата обнаруживается и дополнительное свойство: все пары чисел, расположенные симметрично относительно центральной клетки, дают одинаковые суммы. Магические квадраты, обладающие таким свойством, называются симметрическими. Например,1+25=19+7=18+8=23+3=6+20=2+24=4+22 и т. д.
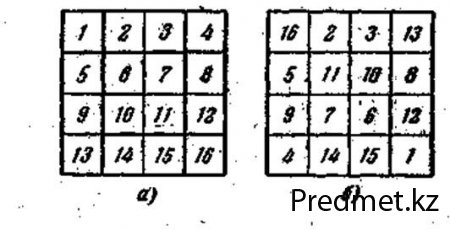
Квадраты порядка, кратного четырем (n=4k).
Для составления какого-либо магического квадрата порядка n=4, 8, 12, …,4k удобна, например, такая простая схема:
1) разместить числа в клетках заданного квадрата в порядке их возрастания (в натуральном порядке);
2) выделить по углам заданного квадрата четыре квадрата со сторонами n/4 и в центре один квадрат со стороной n/2;
3) поменять местами числа, расположенные на диагоналях: 6 и 11, 10 и 7, 1 и 16, 4 и 13.
Великий ученый Пифагор, основавший религиозно-философское учение, провозгласившее количественные отношения основой сущности вещей, считал, что сущность человека заключается тоже в числе – дате рождения. Поэтому с помощью магического квадрата Пифагора можно познать характер человека, степень отпущенного здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования.
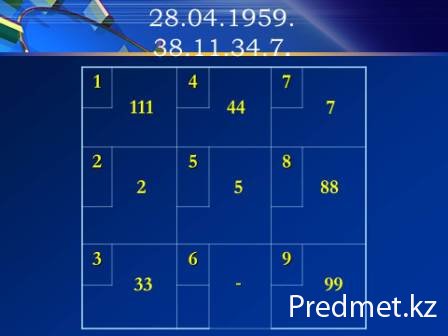
Для того чтобы понять, что такое магический квадрат Пифагора и как подсчитываются его показатели, сделаем расчет. Возьмем дату рождения 20.08.1986. Сложим цифры дня, месяца и года рождения (без нулей): 2+8+1+9+8+6=34. Далее складываем цифры результата: 3+4=7. Затем из первой суммы вычитаем удвоенную первую цифру дня рождения: 34-4=30. И вновь складываем цифры последнего числа: 3+0=3. Осталось сделать последние сложения — 1-й и 3-й и 2-й и 4-й сумм: 34+30=64, 7+3=10. Получили числа 20.08.1986, 34, 7, 30, 64, 10.
И составляем магический квадрат так, чтобы все единицы этих чисел вошли в ячейку 1, все двойки – в ячейку 2 и т.д. Нули при этом во внимание не принимаются. В результате квадрат будет выглядеть следующим возрастом.
|
44 |
9 |
2 |
|
33 |
— |
7 |
|
88 |
11 |
66 |
Ячейки квадрата означают следующее:
Ячейка 1 – целеустремленность, воля, упорство, эгоизм.
1 – законченные эгоисты, стремятся из любого положения извлечь максимальную выгоду.
11 – характер, близкий к эгоистическому.
111 – «золотая середина», Характер спокойный, покладистый, коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким характером подходят на роль военных – профессионалов, а женщины держат семью в кулаке.
11111 – диктатор, самодур.
111111 – человек жестокий, способный совершить невозможное; нередко попадает под влияние какой-то идеи.
Ячейка 2 – биоэнергетика, эмоциональность, душевность, чувственность. Количество ячеек определяет уровень биоэнергетики.
Двоек нет – открыт канал для интенсивного набора биоэнергетики. Эти люди воспитаны и благородны от природы.
2 – обычные в биоэнергетическом отношении люди. Такие люди очень чувствительны к изменениям в атмосфере.
22 – относительно большой запас биоэнергетики. Из таких людей получаются хорошие врачи, медсестры, санитары. В семье таких людей редко у кого бывают нервные стрессы.
222 – знак экстрасенса.
Ячейка 3 – точность, конкретность, организованность, аккуратность, пунктуальность, чистоплотность, скупость, наклонность к постоянному «восстановлению справедливости».
Нарастание троек усиливает эти качества. С ними человеку есть смысл искать себя в науках, особенно точных. Перевес троек порождает педантов, людей в футляре.
Ячейка 4 – здоровье. Это связано с энергетическим пространством, наработанным предками и защищающим человека. Отсутствие четверок свидетельствует о болезненности человека.
4 – здоровье среднее, необходимо закалять организм. Из видов спорта рекомендуется плавание и бег.
44 – здоровье крепкое.
444 и более – люди с очень крепким здоровьем.
Ячейка 5 – интуиция, ясновидение, начинающее проявляться у таких людей уже на уровне трех пятерок.
Пятерок нет – канал связи с космосом закрыт. Эти люди часто ошибаются.
5 – канал связи открыт. Эти люди могут правильно рассчитать ситуацию, извлечь из нее максимальную пользу.
55 – сильно развита интуиция. Когда видят «вещие сны», могут предугадывать ход событий. Подходящие для них профессии – юрист, следователь.
555 – почти ясновидящие.
5555 – ясновидящие.
Ячейка 6 – заземленность, материальность, расчет, склонность к количественному освоению мира и недоверие к качественным скачкам и тем более к чудесам духовного порядка.
Шестерок нет – этим людям необходим физический труд, хотя они его, как правило, не любят. Они наделены неординарным воображением, фантазией, художественным вкусом. Тонкие натуры, они тем не менее способны на поступок.
6 – могут заниматься творчеством или точными науками, но физический труд является обязательным условием существования.
66 – люди очень заземлены, тянуться к физическому труду, хотя как раз для них он не обязателен; желательна умственная деятельность, либо занятия искусством.
666 – знак Сатаны, особый и зловещий знак. Эти люди обладают повышенным темпераментом, обаятельны, неизменно становятся в обществе центром внимания.
6666 – эти люди в своих предыдущих воплощениях набрали слишком много заземленности, они очень много трудились и не представляют свою жизнь без труда. Если в их квадрате есть девятки, им обязательно нужно заниматься умственной деятельностью, развивать интеллект, хотя бы получить высшее образование.
Ячейка 7 – количество семерок определяет меру таланта.
7 – чем больше они работают, тем больше получают впоследствии.
77 – очень одаренные, музыкальные люди, обладают тонким художественным вкусом, могут иметь склонность к изобразительному искусству.
777 – эти люди, как правило, приходят на землю ненадолго. Они добры, безмятежны, болезненно воспринимают любую несправедливость. Они чувствительны, любят мечтать, не всегда чувствуют реальность.
7777 – знак Ангела. Люди с таким знаком умирают в младенчестве, а если и живут, то их жизни постоянно угрожает опасность.
Ячейка 8 – карма, долг, обязанность, ответственность. Количество восьмерок определяет степень чувства долга.
Восьмерок нет – у этих людей почти полностью отсутствует чувство долга.
8 – натуры ответственные, добросовестные, точные.
88 – у этих людей развито чувство долга, их всегда отличает желание помочь другим, особенно слабым, больным, одиноким.
888 – знак великого долга, знак служения народу. Правитель с тремя восьмерками добивается выдающихся результатов.
8888 – эти люди обладают парапсихологическими способностями и исключительной восприимчивостью к точным наукам.
Ячейка 9 – ум, мудрость. Отсутствие девяток – свидетельство того, что умственные способности крайне ограничены.
9 – эти люди должны всю жизнь упорно трудиться, чтобы восполнить недостаток ума.
99 – эти люди умны от рождения. Учатся всегда неохотно, потому что знания даются им легко. Они наделены чувством юмора с ироничным оттенком, независимые.
999 – очень умны. К учению вообще не прикладывают никаких усилий. Прекрасные собеседники.
9999 – этим людям открывается истина. Если у них к тому же развита интуиция, то они гарантированы от провала в любом из своих начинаний.
Итак, составив магический квадрат Пифагора и зная значение всех комбинаций цифр, входящих в его ячейки, вы сможете в достаточной мере оценить те качества вашей натуры, которыми наделила природа.
ЗАКЛЮЧЕНИЕ
В настоящей работе рассмотрены вопросы, связанные с историей развития одного из вопросов математики, занимавшего умы очень многих великих людей, — магических квадратов. Несмотря на то, что собственно магические квадраты не нашли широкого применения в науке и технике, они подвигли на занятия математикой множество незаурядных людей и способствовали развитию других разделов математики (теории групп, определителей, матриц и т.д.).
Ближайшие родственники магических квадратов – латинские квадраты нашли многочисленные применения как в математике, так и в ее приложениях при постановке и обработке результатов экспериментов.
В моей работе так же рассмотрен вопрос о квадрате Пифагора, представляющем исторический интерес и, возможно, полезном для составления психологического портрета личности.
ЛИТЕРАТУРА
1. В.В.Трошин «Магия чисел и фигур» ООО «Глобус» 2007
2. Г.И. Глейзер «История математики в школе» Москва «Просвещение» 2007
3. И.Я.Депман Н.Я. Виленкин За страницами учебника математики «Просвещение» 2006
4. А.П. Доморяд Математические игры и развлечения Москва 1961
5. Интернет ресурсы.

































Скачать урок и презентацию:[attachment=71]
