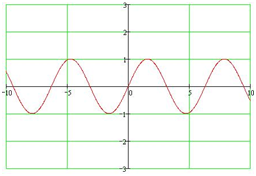
 y=sinx
y=sinx 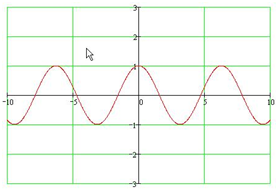 y= cosx
y= cosx
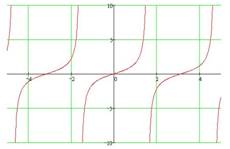 y=tgx
y=tgx 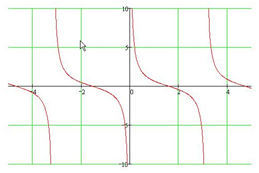 y= ctgx
y= ctgx
№1
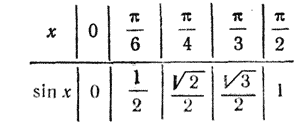
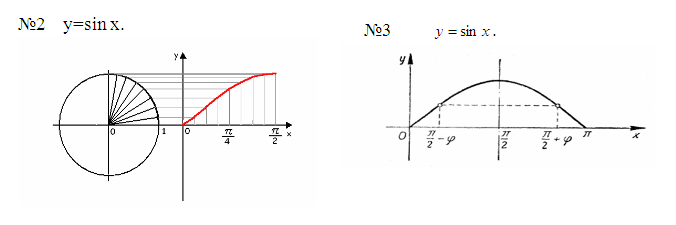
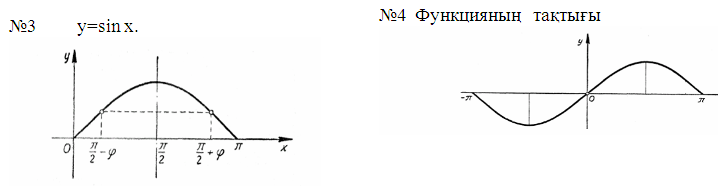
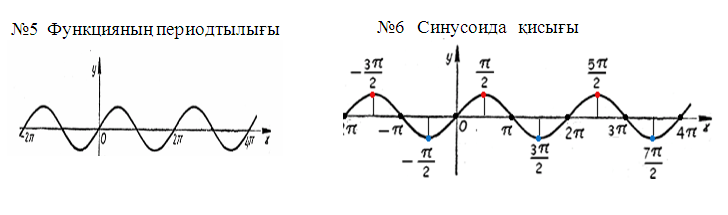
I. y=sin x функциясын қарастырайық.
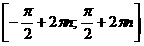 кесінділерінде функция бірсарынды өспелі,
ал
кесінділерінде функция бірсарынды өспелі,
ал 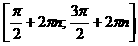 кесінділерінде бір сарынды кемімелі.
кесінділерінде бір сарынды кемімелі.
II. y=cos x функциясын қарастырайық.
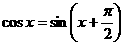 x=0; қадам 0,2 кесте құрып, Еxcel де графиктік диаграмманы таңдаймыз.
x=0; қадам 0,2 кесте құрып, Еxcel де графиктік диаграмманы таңдаймыз.
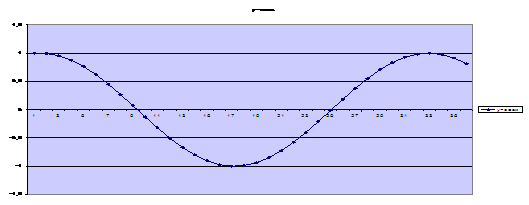
Тригонометриялық функциялардың графиктеріне қарапайым түрлендірулер қолдануға мысалдар
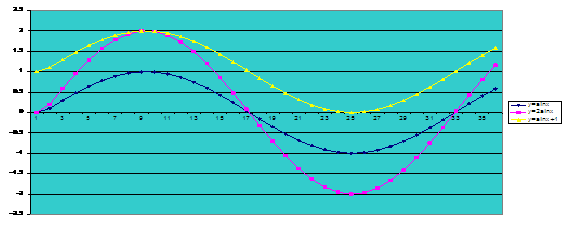
Есептер шығару
Функцияның жұптығын немесе тақтығын анықтаңдар:
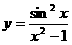
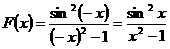 жұп функция
жұп функция
Функциялардың графигін салыңдар y=sin x , y=cos x. функцияларының графиктерін салыңдар
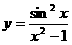
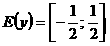

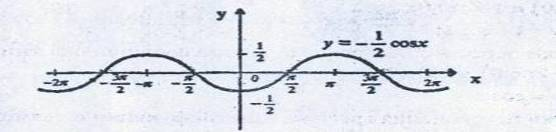
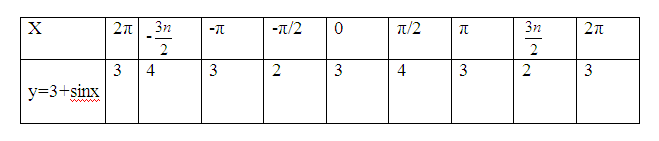
ә) y=3+ sin x.
y=tg x функциясын қарастырамыз:
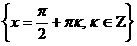 жиынынан басқа барлық нақты сандар жиыны,
себебі
жиынынан басқа барлық нақты сандар жиыны,
себебі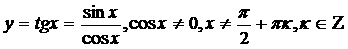
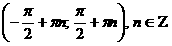 интервалында функция бірсарынды өспелі.
интервалында функция бірсарынды өспелі.
Енді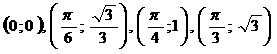 бақылау нүктелерін координаталық жазықтықта белгілеп,
бақылау нүктелерін координаталық жазықтықта белгілеп,
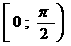 аралығында графигін саламыз. (1-сурет)
аралығында графигін саламыз. (1-сурет)
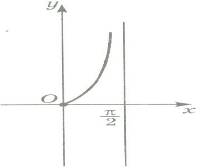 1-сурет
1-суретy=tg x функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық екенін ескеріп,
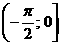 аралығында графикті жалғастырамыз. Сонда y=tg x функциясының
аралығында графикті жалғастырамыз. Сонда y=tg x функциясының
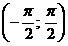 интервалындағы графигі шығады. (2-сурет)
интервалындағы графигі шығады. (2-сурет)
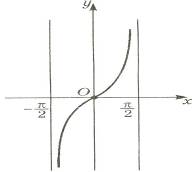 2-сурет
2-суретБерілген функцияның тақ екенін ескеріп, функияның барлық анықталу облысындағы графигін саламыз. (3-сурет)
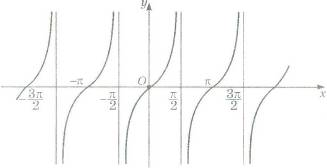 3-сурет
3-суретy=tg x функциясының графигін тангенс оида қисығы деп атайды.
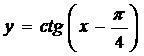 ә)
ә)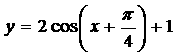
Шешуі: а) Алдымен y = ctg x функциясының графигін саламыз. Графикті Ox осі
бойымен 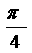 қашықтығына оң бағытқа параллель көшіреміз. (4-сурет)
қашықтығына оң бағытқа параллель көшіреміз. (4-сурет)
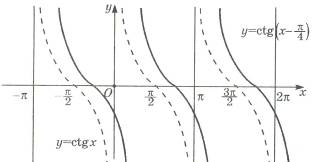 4-сурет
4-суретә) y=cos x функциясының графигін саламыз. Содан кейін Oy осі бойымен графикті 2 есе созамыз. Шыққан графикті Ox осі бойымен
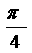 арақашықтығына теріс бағытта параллель көшіреміз. Ең соңғы графикті Oy осі
бойы-мен жоғары бір бірлікке параллель көшіреміз. (5-сурет)
арақашықтығына теріс бағытта параллель көшіреміз. Ең соңғы графикті Oy осі
бойы-мен жоғары бір бірлікке параллель көшіреміз. (5-сурет)
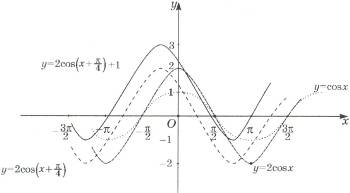 5-сурет
5-сурет