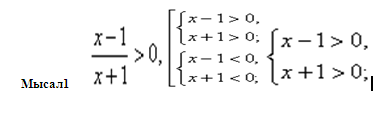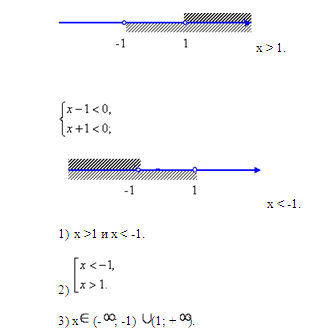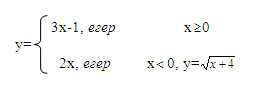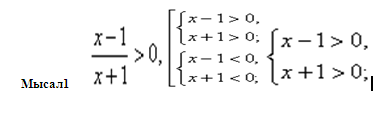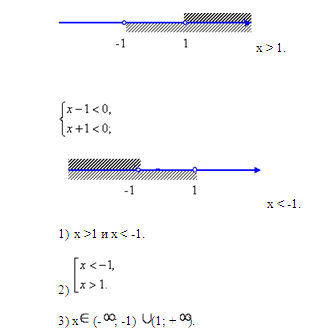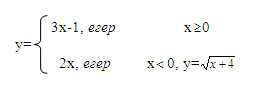A санының b санынан үлкен (кіші) екендігін көрсету үшін a>b (a < b) жазамыз
Мысалдар.
5>2, 3>0, 7<9, 100<150, -2>-3
Үлкен>, кіші<белгілерімен қатар үлкенне тең ≥ және кішіне тең ≤ деген белгілері қолданылады.
a ≥ b (a ≤ b) деген белгілеуі a санының b санынан үлкен (кіші) не оған тең болуын көрсетеді.
>, < , ≥ , ≤ белгілері теңсіздік белгілері деп аталады.
Өрнектің сол және оң жағы теңсіздік белгісімен байланысса онда бұндай өрнекті теңсіздік деп атаймыз.
Теңсіздіктердің қасиеттері:
1). a > b, c > d болса онда a+c > c+d.
Мысалы 7 > 5, 3 > 2 соңдықтан 7+3 > 5+2.
2). a ≥ b, c ≥ d болса онда a+c ≥ c+d.
3). a > b болса онда -a < -c.
Мысалы 2>1, -2<-1.
4). a ≥ b болса онда -a ≤ -c.
5). a > b болсын, k саны оң болса онда k • a>k • b, k саны теріс болса онда k • aМысалы 3 > 2, 4•3 > 4•2, -4•3 < -4•2.
6). a ≥ b болсын, k саны оң болса онда k • a ≥ k • b, k саны теріс болса онда k • a ≤ k • b.
f(x) > g(x), f(x) < g(x), f(x) g(x), f(x) g(x).