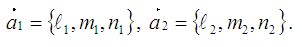№ 40 Түзудің теңдеуі. Бір нүктеден, екі нүктеден өтетін түзулердің теңдеуі. Түзулердің арасындағы бұрыш. Түзулердің өзара параллель немесе перпендикуляр болуы туралы шарттар.

Жазықтықтағы түзулер
Тікбұрышты декарттық жүйеде екі айнымалыдан тәуелді кез келген сызықты теңдеу жазықтықта түзуді анықтайды.

Ax+By+C=0

түзудің жалпы теңдеуідеп аталады.

Абсцисса өсінің оң бағыты мен берілген түзудің арасындағы α бұрышы түзудің көлбеулік бұрышы деп аталады. Бұл бұрыш абсцисса өсінің оң бағытынан басталып есептелінеді және бұрышты есептеу сағат тілінің қозғалу бағытына қарсы болса «+» таңбасымен, кері жағдайда «-» таңбасымен алынады. Көлбеулік бұрыштың тангенсі түзудің бұрыштық коэффициенті деп аталады. Әдетте, бұл коэффициент k=tgα деп белгіленеді.

Түзудің жазықтықта берілу тәсілдері:

1)Бұрыштық коэффициенті k және түзудің ордината өсінен қиып өтетін b кесіндісі арқылы берілген түзу

y= kx+b

теңдеуі арқылы анықталаы (8-сурет).

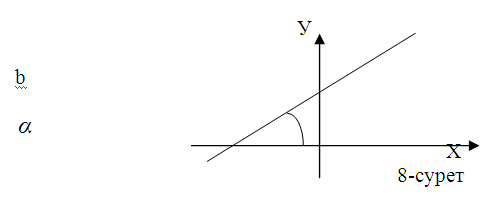
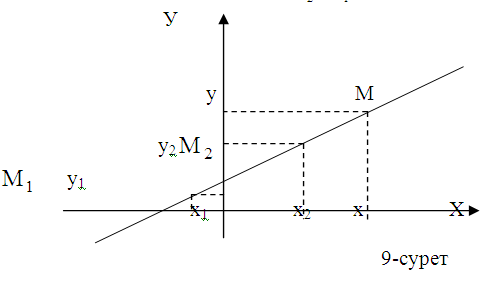
2)Түзудің бойында жатқан M1( x1; y1)және M1( x1; y1) нүктелері арқылы өтетін түзу

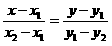
теңдеуі арқылы анықталады.

Бұрыштық коэффициенті 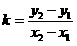формула арқылы есептеледі (9-сурет).

3) Координат өстерінен қиып өтетін а және b кесінділері арқылы өтетін түзу

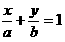
теңдеуі арқылы анықталады. (10-сурет) және бұл теңдеу түзудің кесінділердегі теңдеуі деп аталады, (мұндағы а –Ох өсінен, b –Oу өсінен түзудің қиып өтетін кесінділері).

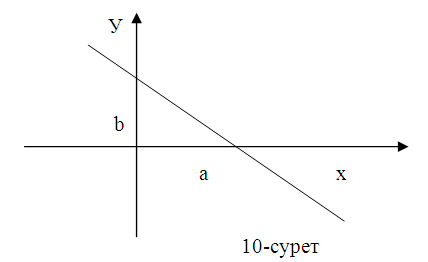
4) Координат басынан түзуге түсірілген нормаль арқылы анықталған түзу(11-сурет).

Егер осы нормальдің табаны Р нүктесінде жатып, ОРкесіндісі Ох өсімен α бұрышын жасаса және ұзындығы р-ға тең болса, онда түзу

x* cosα + y* sin α – p = 0

теңдеуі арқылы анықталады. Бұл теңдеу түзудің нормаль теңдеуі деп аталады.

Егер түзу нормаль теңдеуі арқылы берілсе, онда M(x*, y*) нүктесінің осы түзуден ауытқуы

δ= x*cosα + y * sinα

формуласы арқылы есептеледі. Нүктеден түзуге дейінгі қашықтық осы ауытқудың абсолют шамасына тең: d= |δ|.

Түзудің жалпы теңдеуін нормаль түріне келтіру үшін, осы теңдеудің барлық мүшелері

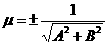
формуласы арқылы анықталған нормаль көбейткішке көбейтіледі. Нормаль көбейткіштің таңбасы жалпы теңдеудегі бос мүшенің таңбасына кері болады.

Түзудің толық емес теңдеулері:

1) Егер түзудің жалпы теңдеуіндегі бос мүше С=0 болса, онда теңдеу
Ax+By=0
түрінде жазылады да түзу координат басы арқылы өтеді;

2) Егер түзудің жалпы теңдеуіндегі B= 0(A ≠ 0) болса, онда теңдеу

Ax+C = 0
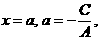түрінде жазылады да түріне келтіріледі.Бұл түзу ординат өсіне параллел болып, абсцисса өсінен а-ға тең кесіндіні қиып өтеді;

3) Егер түзудің жалпы теңдеуіндегі A= 0(B ≠ 0) болса, онда теңдеу

By+ C = 0

түрінде жазылады да 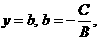түріне келтіріледі. Бұл түзу абсцисса өсіне параллель болып, ординат өсінен b-ға тең кесіндіні қиып өтеді;

4) Егер түзудің жалпы теңдеуіндегі B = 0, C= 0(A≠ 0) болса, онда теңдеу

x=0
түрінде жазылады да ординат өсін анықтайды;

5) Егер түзудің жалпы теңдеуіндегі A = 0, C= 0(A≠ 0) болса, онда теңдеу

y=0
түрінде жазылады да абсцисса өсін анықтайды;

6) Егер түзудің жалпы теңдеуінің барлық коэффициенттері нөлге тең болмаса, онда жалпы теңдеу

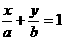
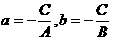түріне келтіріледі. Бұл түзудің кесінділердегі теңдеуі. Мұндағы болады да абсцисса өсінен а-ға тең және ординат өсінен b-ға тең кесінділерді қиып өтеді.

Егер екі түзудің k1 және k2 бұрыштық коэффициенттері белгілі болса, онда осы түзулердің арасындағы бұрыш

формуласы арқылы анықталады.

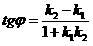
Егер екі түзу A1x+ B1y+ C1=0 және A2x+ B2y+ C2=0 жалпы теңдеулері арқылы берілсе, онда бұл түзулердің бұрыштық коэффициенттері

формулалары арқылы анықталады.

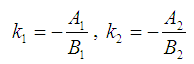
Түзулер өзара параллель болуы үшін

k1=k2,
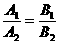демек шарттары орындалу керек.

Түзулер өзара перпендикуляр болуы үшін

k1*k2 = -1,
немесе
демек
A1A2+B1B2=0,
шарттары орындалу керек.

Егер

болса, түзулер параллель болады, ал
болса, онда түзулер беттеседі.

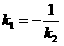
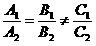
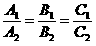
Егер түзулер бір S нүктесінде қиылысса, онда α (A1x+B1y+ C1)+β(A2x+ B2y+C2)=0,теңдеуі центрі S нүктесінде жатқан түзулер шоғын анықтайды.

Мұндағы α мен β кез келген нақты сандар. Егер α ≠ 0 болса, онда 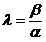деп алып, теңдеуі (A1x+B1y+ C1)+λ(A2x+ B2y+C2)=0, түріне келтіріледі. Бұл теңдеу, A2x+ B2y+C2)=0 түзуінен басқа, S нүктесі арқылы өтетін кез келген түзуді анықтайды.

Кеңістіктегі жазықтықтар

Бірінші дәрежелі теңдеу декарттық координаттар бойынша кеңістіктегі жазықтықты анықтайды және, керісінше, кез келген жазықтық бірінші дәрежелі теңдеу арқылы анықталады. Бұл теңдеу
Ах+Ву+Сz+D=0
түрінде жазылады да, жазықтықтың жалпы теңдеуі деп аталады. Мұндағы А,В,С,D – нақты сандар.

Кеңістікте жазықтықты анықтайтын белгілер:

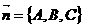1)Берілген M0(x0,y0, z0) нүктесі арқылы өтетін нормаль векторы болатын тек қана бір жазықтық бар болады. Бұл жазықтықтың теңдеуі
A(x - x0) + B(y- y0)+C(z- z0)=0,
түрінде жазылады.

2) Бір түзудің бойында жатпайтын M1( x1, y1, z1), M2( x2, y2, z2), және M3( x3, y3, z3), нүктелері арқылы тек қана бір жазықтық жүргізуге болады. Бұл жазықтықтың теңдеуі

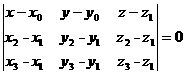
3) Координат өстерінен нөлге тең емес a,b,c кесінділерін қиып өтетін теқ қана бір жазықтық бар болады. Бұл жазықтықтың теңдеуі

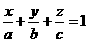
түрінде жазылады да жазықтықтың «кесінділердегі» теңдеуі деп аталады.

4) Координат басынан шығып, берілген жазықтыққа перпендикуляр болатын векторы, осы жазықтықты Р нүктесінде қиып өтсін және векторымен бағыттас болсын (егер Р координат басында жатса, демек, жазықтық координат басы арқылы өтсе, онда n векторының оң бағыты еркін таңдалады).

векторының бағыттауышы косинустары cosα, cosβ, cosγ болып, болса, онда жазықтықтың теңдеуі

x*cosα+y* cosβ+z* cosγ – p = 0
түрінде жазылады да осы жазықтықтың нормаль теңдеуі деп аталады.

Кез келген M*( x*, y*, z*), нүктесі үшін δ=x *cosα + y*cosβ + z*cosγ - p саны M* нүктесінің берілген жазықтықтан ауытқуыдеп аталады.

Егер δ>0 болса, онда M* жазықтықта, δ>0 болса M* мен координат басы жазықтықтың екі жағында, ал δ<0 болса бір жағында жатады.

M*( x*, y*, z*) нүктесінен жазықтыққа дейінгі қашақтық d=|δ| болады.

Егер жазықтық жалпы теңдеуі арқылы берілсе, онда 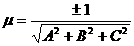саны нормалдаушы көбейткішдеп аталады. Нормалдаушы көбейткіштің таңбасы μ*D<0 шарты орындалатындай етіп таңдалады.

Жалпы теңдеуді нормаль түрге келтіру үшін, осы теңдеу нормаль көбейткішке көбейтіледі де μ(Ax+By+Cz+D)=0 жазықтықтың нормаль теңдеуі болады.

Жазықтықтың толық емес теңдеулері:

1) Егер D=0 , болса, онда жазықтықтың жалпы теңдеуі Ax+By+Cz=0 түрінде жазылады да жазықтық координат басы арқылы өтеді;
2) Егер С=0 , болса, онда жазықтықтыњ тењдеуі Ax+By+D=0 түрінде жазылады да Оz осіне параллель болады;
3) Егер В=0 және С=0 болса, онда жазықтық Ax+D=0 теңдеу түрінде жазылады да Оуz координат жазықтығына параллель болады;
4) Егер жалпы теңдеудің барлық коэффициенттері нөлге тең болмаса, онда теңдеу

түріне келтіріледі.

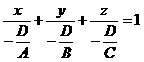
Мұндағы 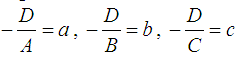сандары жазықтықтың

координат өстерінен қиып өтетін кесінділердің шамасын анықтайды.
Жазықтықтырдың кеңістіктегі өзара орналасуы:
Кеңістіктегі екі жазықтық өздерінің жалпы теңдеулері:

арқылы берілсін.

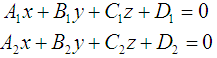
Егер

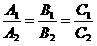
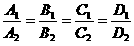
болса, онда жазықтықтар өзара параллель болады, ал егер
болса, онда жазықтықтар беттеседі.

Өзара параллель болмайтын екі жазықтық түзу бойымен қиылысады.

α(A1x+ B1y+ C1z+ D1)+β(A2x+ B2y+ C2z+ D2)= 0
теңдеуі (α,β-нақты параметрлер) кеңістікте бір түзу арқылы өтетін барлық жазықтықтарды анықтайды да жазықтықтар шоғының теңдеуі деп аталады.

Коэффициенттері A1A2+B1B2+ C1C2=0 шартын қанағаттандыратын екі жазықтық өзара перпендикуляр болады.

Жазықтықтардың 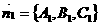және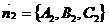нормаль векторлары арасындағы бұрыш жазықтықтар арасындағы екі жақты бұрышдеп аталады да

формуласы арқылы анықталады.

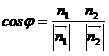
Кеңістіктегі түзу

Берілген
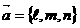M0( x0, y0, z0), нүктесі арқылы, берілген векторына параллель тек қана бір түзу жүргізуге болады. Бұл түзудің теңдеуі

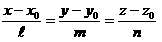
түрінде жазылады.

Мұндағы 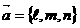түзудің бағыттауыш векторыдеп аталады да оның координаттары 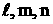түзудің бағыттауыш параметрлері, ал бағыттауыш косинустары осы түзудің бағыттауыш косинустары деп аталады. теңдеуі түзудің канондық теңдеуідеп аталады.

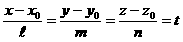
деп алып (t-нақты параметр), түзудің теңдеуін

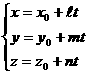
түріне келтіреміз. Теңдеудің бұл түрі параметрліқ теңдеу деп аталады. M(x,y,z) түзу бойындағы ағымдағы нүкте болса, онда теңдеуі 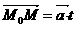t ϵ ( - ∞ ; + ∞) түрінде жазылады. Бұл теңдеу түзудің векторлық теңдеуідеп аталады.

Егер түзу өзінің бойымен қиылысатын екі жазықтықтың жалпы теңдеулері арқылы берілсе

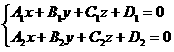
онда түзудің бағыттауыш векторы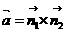болады. Мұндағы 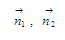осы жазықтықтардың нормаль векторлары. Түзудің бағыттауыш параметрлері

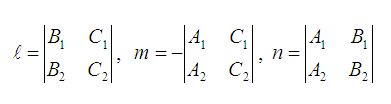
формулалары арқылы анықталады. Егер M0( x0, y0, z0), осы түзудің бойындағы белгіленген нүкте болса, онда теңдеулер жүйесі арқылы берілген түзудің теңдеуін канондық, параметрлік немесе векторлық түрінде жазуға болады.

Мысалы, түзу өзара қиылысатын екі жазықтықтың теңдеулері арқылы берілсін

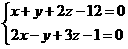
x0=1 деп алып, осы түзудің бойында жатқан M(1,7,2) нүктесін табамыз.

Жазықтықтың нормаль векторлары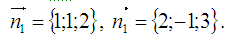

Түзудің бағыттауышы векторы 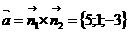Сондықтан, канондық теңдеуі

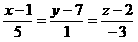
параметрлік теңдеуі

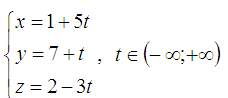
векторлық теңдеуі

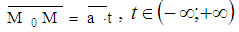
Мұндағы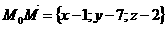

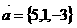
Кеңістіктегі кез келген M1( x1, y1, z1), M2( x2, y2, z2), нүктелері арқылы тек қана бір түзу жүргізуге болады. Бұл түзудің теңдеуі

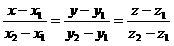
түрінде жазылады да екі нүкте арқылы өтетін түзудің теңдеуі деп аталады.

Кеңістікте канондық теңдеулері арқылы

екі түзу берілген.

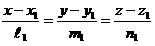
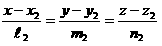
Бұл түзулердің бағыттауышы векторлары