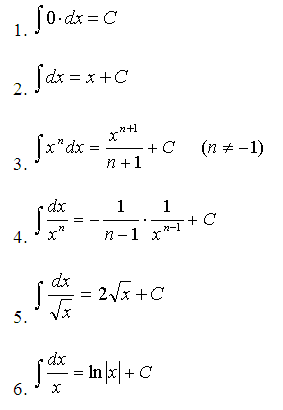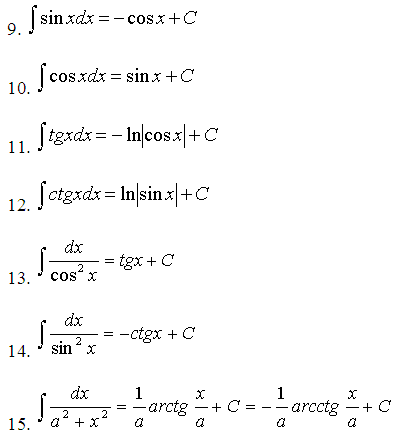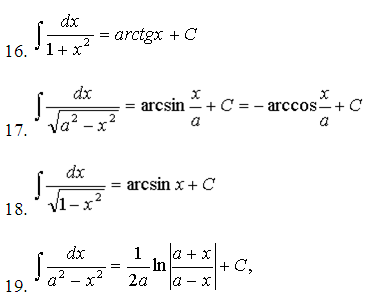3. Интеграл таңбасы астындағы функцияны түрлендіру және интеграл қасиеттерін пайдалану нәтижесінде бір немесе бірнеше интегралдар есептеуге тура келеді.
Егер ∫ f(x) dx = F(x) + C болса, онда Егер ∫ f(u) dx = F(u) + C орындалады.
Мұнда x аргументі жаңа u аргументімен ауыстырылған. Интеграл берілген күйінде кестелік интегралға келмейтін кезде көптеген жағдайларда, интеграл астындағы өрнекті түрлендіру арқылы оны кестелік интегралға келтіруге болады. Мұндай жағдайда қандай түрлендіру жүргізу керек екенін білу қажет.
Егер интеграл ∫ [f(x)]αφ(x)dx түрінде беріліп, φ(x) = kf ꞌ (x) (k = const) теңдігі орындалса, онда интегралды кестелік интегралға келтіруге болады, яғни
∫[f(x)]αφ(x)dx =∫ [f(x)]αkf ꞌ (x)dx = k ∫ [f(x)]αdf(x)