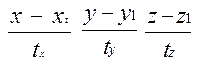
№ 63 Түзулер мен жазықтықтардың перпендикулярлығы. Түзу мен жазықтықтың өзара параллель және перпендикуляр болуы арасындағы байланыс.

Түзудің векторлық теңдеуін қолданып, оның координаталық теңдеуін шығаруға болады. Жоғарыда қарастырылып отырған R-R1 және t векторлары параллель болғандықтан, олардың осьтерге түскен проекциялары өзара пропорционал болады:

Енді tx=m, ty=n, tz=l деп белгілесек, онда теңдеу былайша жазылады:

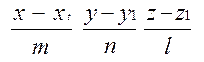
мұндағы М1М={ x-x1, y-y1, z-z1 } және t={m,n,l} векторлары өзара коллинеар болғандықтан, олардың проекциялары өзара пропорционал болады. Бұл (4) теңдеу кеңістіктегі түзудің жабайы теңдеуі деп аталады.

Кеңістіктегі екі нүктеден өтетін түзудің теңдеуі.

М1(x1, y1, z1) және М2(x2, y2, z2) нүктелері берілсін. Түзу М1(x1, y1, z1) нүктесінен өтеді және бағыттаушы М1М2={x2-x1, y2-y1, z2-z1} векторына параллель. Сондықтан (4) теңдеу бойынша екі нүктеден өтетін түзудің теңдеуін табамыз:

Екі түзудің бір жазықтықта жату шарты.

Екі түзу жабайы теңдеулермен берілсін :

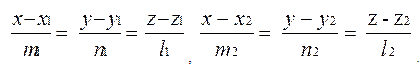
Бұл екі түзу бір жазықтықта жатса, онда мына

М1М={ x2-x1, y2-y1, z2-z1 } , t1={m1, n1, l1}, t2={m2, n2, l2} векторлары өзара компланар болады. Сондықтан бұл үш вектордың аралас көбейтіндісі нольге тең :

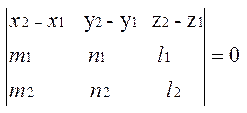
) теңдік екі түзудің бір жазықтықта жату шартын көрсетеді.

Екі жазықтықпен берілген түзудің теңдеуі.

Екі жазықтық жалпы теңдеулермен берілсін :
A1x+ B1y+ C1z+D1=0 ,
A2x+ B2y+ A1z+D2=0

Бұлардың коэфициенттерінен екі матрица құрайық :

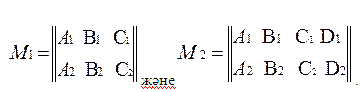
Осыған сәйкес рангілерді белгілейік :R1(M1), R2(M2). Егер бірінші матрицаның рангісі екіге тең болса (R1(M1)=2) , онда екінші матрицаның рангісі де екіге тең: R2(M2)=2. Сондықтанда өз ара параллель болмайтын бұл екі жазықтық бір түзудің бойымен қиылысады. Сөйтіп, егер

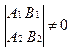
онда екі жазықтықтың қиылысқан түзуінің бойындағы кез келген нүктенің координаталары екі жазықтықтыңда теңдеуі кеңістіктегі бір түзуді анықтайды. Шындығында, бір түзудің бойымен жүргізілген жазықтықтарды жазықтықтар шоғы дейміз. Осы жазықтықтар шоғындағы әр бір екі жазықтықтың жиындысы әрқашанда бір түзуді кескін дейді. Жоғарғы (7) теңдеулерден x пен y-тің мәндерін z арқылы өрнектейік:

Екі түзудің арасындағы бұрыш. Екі түзудің перпендикулярлық және параллельдік шарттары.

Екі түзу берілсін:

Осы екі түзудің арасындағы бұрышты іздейік.

Бірінші түзудің осьтерімен жасайтын бұрыштары α1,β1,γ1, екінші түзудің сол осьтермен жасайтын сәйкес бұрыштары α2,β2,γ2, болса, онда олардың бағыттаушы косинустары мынадай болады. (7-пункттегі (15) формула):

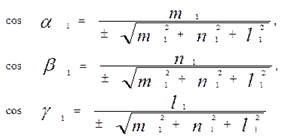
Екі түзудің арасындағы бұрышты φ деп белгілесек, онда екі вектордың арасындағы бұрышты анықтайтын формула бойынша (векторлық алгебра):

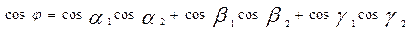
осыған (18) теңдеулердегі косинустардың мәндерін қояйық:

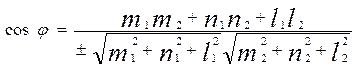
Айқасқан екі түзудің арасындағы бұрыш деп, берілген екі түзуге параллель болатын, кеңістіктің кез келген нүктесінен жүргізілген екі түзудің арасындағы бұрышты айтамыз. Бұл бұрыш бірін- бірі 180 Ә- қа толықтыратын және сол 180 Ә-тан әрқашанда кем болатын екі бұрыштың біреуі болады.

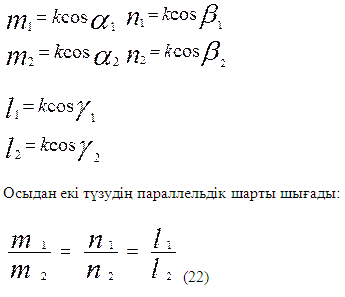
Екі нүктеден өтетін түзудің теңдеулері(екінші әдіс).

Кеңістікте екі нүкте берілсін: M1 (x1,y1, z1), M2 (x2,y2, z2). Осы екі нүктеден өтетін түзудің теңдеулерін іздейік. Кеңістікте берілген бір нүктеден өтетін түзудің теңдеулері бізге мәлім:

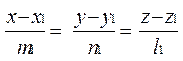
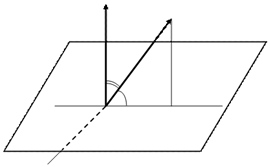
Түзу мен жазықтықтың арасындағы бұрыш.

(157-сызба)

<

Түзу мен жазықтықтың қиылысуы.

Түзу мен жазықтықтың теңдеулері берілсін:

Осы түзу мен жазықтықтың қиылысатын нүктесін табайық.

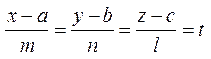
Түзу мен жазықтық бір нүктеде қиылысса, онда осы нүктенің координаталары берілген түзу мен жазықтықтың теңдеулерін қанағаттандырады. Сондықтан:

Осыдан үш теңдік шығады:

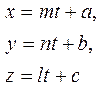
Нүктеден түзуге дейінгі ара қашықтық.