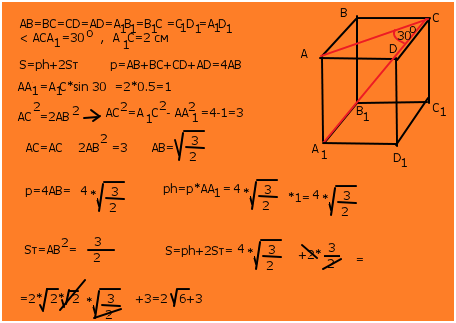
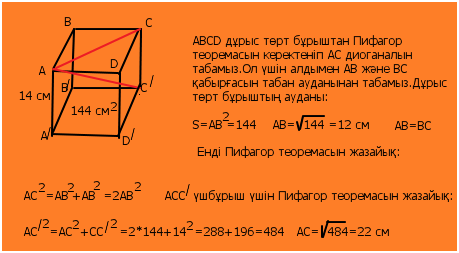
Бұл фигуралар көпжақтардың призмалар деп аталатын тобына жатады.
Анықтама. Екі жағы параллель жазықтықтарда жататын өзара тең көпбұрыштар,ал қалған жақтары осы көпбұрыштармен ортақ қабырғалары бар параллелограмдарболып келген көпжақты призма деп атайды.
А1А2…Ап мен В1В2… Вп
көпбұрыштары мен п – параллелограмнан құралған көпжақ призма деп аталады. Призманың табандары,
бүйір жақтары,бүйір қырлары.
Призма: тік призма, көлбеу призма.
Анықтама: Бүйір қырлары табандарына перпендикулярпризмалар тік призмалар деп аталады.
Анықтама:Әрі тік,әрі табаны дұрыс көпбұрыш болатын призманы дұрыс призма деп атайды.
Анықтама: Табаны параллелограмм болатын призманы параллелепипед деп атайды.
Теорема:Параллелепипедтің диагональдары бір нүктеде қиылысады және осы нүктеде қақ бөлінеді.
Анықтама:Бүйір қырлары табан жазықтығына перпендикуляр ,ал табандары тіктөртбұрыштар болып келген параллелепипед тікбұрышты параллелепипед деп аталады.
Теорема:Тік бұрышты параллелепипедтің диагоналінің квадраты оның үш өлшемінің квадраттарының қосындысына тең.
АС12=АВ2+ВС2+СС12
Көпжақтың қиюшы жазықтықтарының орналасуына қарай қимада әртүрлі көпбұрыштар болуы мүмкін.
тік параллелепипед
Sб=Ро*h, мұндағы Ро —периметр, h — биіктік
Sп=Sб+2Sо, Sо — табан ауданы
Көлем V=Sо*h
Sб=2c(a+b), a, b — , c — кабырға параллелепипедаSп=2(ab+bc+ac)
Көлем V=abc, где a, b, c — параллелепипеда.
Куб:S= 6a 2
көлем : V = a3 , a — кубтың қабырғасы.