№ 72 Цилиндрдің, конустың, қиық конустың, шардың, шардың бөліктерінің көлемі

Барлық нәрселердің негізгі болып табылатын ең жай формалар – геометриялық денелер. Олар куб, цилиндр, конус, призма, пирамида т. б.

Цилиндр - Тұйық цилиндрлік бетпен және өзара параллель екі жазықпен шектелген геометриялық дене.

Цилиндр тіктөртбұрыш - тан және екі дөңгелектен тұрады. Тіктөртбұрыштың бір қабырғасы цилиндрдің биіктігіне басқа қабырғасы цилиндр табанындағы шеңбердің ұзындығына тең. Құмыра бірнеше геометриялық фигуралардан тұрады. Денелерді көшіре салмай, дененің құрылымына, оның геометриялық құрылысына талдау жасау керек. Бейнелейтін нәрсенің сыртқы пішіні жарық пен көлеңке арқылы айқындалады. Олардың белгілі атаулары бар.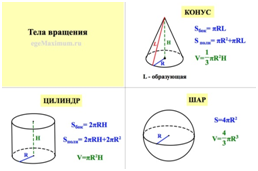

Сфера (гр. sphaіra – шар) математикада – барлық нүктелері бір нүктеден (сфера центрінен) бірдей қашықтықта болатын тұйық бет. Сфера центрін оның кез келген бір нүктесімен қосатын кесінді (сондай - ақ оның ұзындығы) сфераның радиусы деп аталады. Сфера бетінің ауданы: S = 4pR2, мұндағы R – сфера радиусы. Сферамен шектелген әрі центрі бар кеңістіктің бөлігі шар деп аталады. Шардыңкөлемі: V = 3/4pR3

Шар бетін жазықтыққа жазып тас тау мүмкін емес. Сондықтан оның анықтамасын шек түсінігін пайдаланып беруге болады.

Теорема: Шар бетінің ауданы төрт еселенген үлкен дөңгелектің ауданына тең. Дәлелдеу. Үлкен дөңгелек ауданы S = πR2
Проблема:
3) Шар беті сфераны қалай аламыз? Плакаттан көрсету.
Жауап: Центрі О нүктесі болатын, диаметрі АҒ – ге тең жарты шеңбер берілсе, оны АҒ диаметрінен айналдырсақ шар бетін – сфераны аламыз.
4) Жарты шеңберге қабырғалар саны n-ге теңАВСДЕҒ дұрыс сынық сызықты іштей сызамыз. АҒ – диаметрінен айналдырсақ шыққан бет сфера бетіне шамалас болады. Сынық сызықтар санын арттырсақ, онда жуықтау дәлірек болып сфера бетіне жақындай түседі.
5) Шар бетінің ауданының анықтамасын береміз.
Анықтама .Жарты шеңберді оның диаметрінен айналдырған да шығатын шар бетінің ауданы ретінде жарты шеңберге іштей сызылған дұрыс сынық сызықты сол диаметрден сынық сызықтың буындар санын шексіз көбейте отырып айналдырғанда шығатын бет ауданының ұмтылатын шегі алынды.
6) Сынық сызықты айналдырғанда (конус, қиықконус, цилиндр беттерінен тұрады).
7) Іштей сызылған сынықтың апофемасын а деп белгілейік. Айналу денелерінің бүйір беттерінің аудандарының жалпы формуласы бойынша
Sб.б.= H 2 Па
8) АВ буыны айналғанда шығатын беттің ауданы АК * 2 Па
ВС буыны айналғанда шығатын беттің ауданы KN * 2 Па
СД буыны айналғанда шығатын беттің ауданы NP * 2 Па
ДЕ буыны айналғанда шығатын беттің ауданы PQ * 2 Па
ЕҒ буыны айналғанда шығатын беттің ауданы QF * 2 Па
9) Осыларды қосып АВСДЕҒ сынығының АҒ осінен айналғанда шығатын беттің ауданын аламыз. 2 Па (АК + KN + NP + PQ + QF) = 2 Па * АҒ
10) Буындар санын шексіз көбейтсек, сынық сызықтың бетінің ауданы, шар бетінің ауданына, ал апофемасы берілген жарты шеңбердің радиусына ұмтылады. Радиусы R десек. АҒ = 2 R.
S шар беті = 2 ПR * 2R = 4 ПR2
11) АС доғасы АҒ осінен айналғанда шығатын шар сегменті бетінің ауданын есептеу формуласын қорытып шығару.
АВ + ВС + АК * 2 Па
KN * 2 Па
2 Па (АК + KN) = 2 Па * AN = 2 ПR * h
S шарсег. = 2 ПRh

Сфералық белдіктің ауданын есептеу формуласын табайық. һ = һ2 – һ1 шар қабатының сфералық бетін биіктіктері һ1 және һ2 болатын екі сегмент беттерінің айырмасы деп қарастыруға болады.

S шарқаб. = 2 ПR (h2 – h1) = 2 ПRh
S шарқаб. = 2 ПRh

Шардың көлемімен бетінің ауданы туралы Архимедте өз тұжырымын жасаған: Ол «шардың көлемімен бетінің ауданы, оған сырттай сызылған цилиндрдің көлемімен толық бетінің ауданының 2/3 бөлігіне тең» деп тұжырымдаған.

Сфера және шар олардың бөліктері сфералық геометрия деп аталған. Сфералық геометрия астрономияда кеңінен қолданылады, сонымен қатар теңіз кемелерінің, самолет және космос кораблдерінің штурмандары жұлдыздарға қарап, өз координаталарын анықтайды. Жердің шар тәрізді екенін ескере отырып, шахта, метрополитень, тоннель құрылыстарында және жер шарының бетінің иодезиялық түсірілімдерінде (съемка) кеңінен қолданылады.

Конус (лат.conus, гр.'konos' )

1. Конус немесе конустық бет–белгілі бір сызықтың (бағыттаушы) барлық нүктесін кеңістіктің берілген нүктесімен (төбесімен) қосатын түзулердің (жасаушыларының) геометриялық орны. Егер бағыттаушы түзу сызық болса, онда Конус жазықтыққа айналады. Егер бағыттаушы өзінің төбесімен бір жазықтықта жатпайтын 2-ретті қисық сызық болса, онда 2-ретті Конус шығады. Дөңгелек Конус немесе тік дөңгелек Конус 2-ретті Конустың қарапайым түрі, оның бағыттаушысы шеңбер болады, ал төбесі осы шеңбер центріне ортогональ проекцияланады;

2. Элементар геометрияда дөңгелек Конус деп бағытталған шеңбері бар, дөңгелек Конустың бетімен және оның осіне перпендикуляр жазықтық пен шектелген геометриялық денені айтады.

• Конустың ауданы: S=PI RL Бұл жерде— радиусы, — ұзындығы.

• Конустың көлемі: V=1/3 PIR^2 H

Қиық конус — конустың табаны мен осы табанға параллел жазықтықпен қиылып шектелген бөлігі. Басқаша айтқанда толық конустың сүйір ұшы қыр қылып тасталған "мұқыл" конус. Қиық конустың жоғарғы табанынан төменгі табанына түсірілген перпендикуляр сызықтың екі табан аралығындағы кесіндісі оның биіктігі болады.

• Қиық конустың бүйір жағының ауданы мұндағы— қиық конустың жасаушысы, және— сәйкес түрде табандарының радиустары. Толық бетінің (Тб) ауданы бүйір бетінің (б) ауданына қиық конустың жоғарғы табанының (жТ) ауданы мен төменгі табанының ( ТТ)аудандарының қосындысына тең, яғни

• Қиық Қиық конустың бүйір жағының ауданы пирамиданың көлемі: мұндағы— қиық конустың биіктігі.
• Қиық конустың жасаушысы: — қиық конустың төменгі табанының радиусы, — жоғарғы табанның радиусы, — қиық конустың биіктігі.
• Толық конустың биіктігі: