Разноуровневые задания как инструментарий управления познавательной деятельностью учащихся
Попова. И. Я. учитель математики,
Северо-Казахстанская область, Тайыншинский район,
с. Новодворовка, Новодворовская ОШ
Выдвижение и развитие концептуальной идеи планирования обязательных результатов обучения позволило подойти к проблеме дифференцированного подхода с новых позиций. Проблема не является новой для школы, однако, отличие подхода состоит в том, что перед разными категориями учащихся ставятся различные цели: одни ученики должны достичь определенного объективно обусловленного уровня подготовки, называемого базовым, а другие, проявляющие интерес к предмету и обладающие хорошими способностями, должны добиться более высоких результатов.
Особое значение в обучении математике и информатике, как и любому предмету, имеет дифференциация обучения. Такой подход в обучении осуществляю при помощи дидактических материалов, составленных с учетом доминирующих особенностей различных групп учащихся.
В соответствии с этим в классе выделяю три группы учащихся: группа базового (обязательного) уровня, группа повышенного уровня и группа углубленного уровня.
Состав групп может меняться: любой ученик из группы базового уровня переходит в группу повышенного уровня, если он хорошо усвоил материал и свободно выполняет задания, соответствующие обязательным результатам обучения. С другой стороны, ученик из группы повышенного уровня переходит в группу базового уровня, если он имеет пробелы в знаниях или не справляется с темпом продвижения группы.
Разноуровневые задания составляю с учетом требований педагогической технологии уровневой дифференциации обучения учащихся, разработанной на основе научных концепций профессора Ж.А. Караева.
Задания составлены в трёх вариантах:
Вариант А — задания I уровня — каждый учащийся должен уметь решать самостоятельно. Он рассчитан на слабо подготовленных учащихся и ориентирован в основном на достижение учащимися обязательного уровня подготовки, определённого Стандартом образования по предметам. Вариант А содержит большое количество простых тренировочных упражнений с постепенным пошаговым нарастанием трудности. Для многих заданий можно давать ответы, указания, пошаговые инструкции, некоторые данные для самоконтроля.
Он выдается группе учащихся, которые испытывают затруднения при изучении предмета.
Вариант Б — задания 2 уровня — обеспечивают постепенный переход от заданий обязательного уровня к более сложным заданиям. Вариант Б несколько усложнён по сравнению с вариантом А. Он не только способствует достижению учащимися обязательного уровня подготовки, но и создаёт условия для овладения знаниями и умениями на более высоком уровне.
Вариант В — задания 3 уровня — требуют не только свободного владения приобретёнными знаниями, но иногда и творческого подхода, проявления смекалки и сообразительности.. В основном третья группа состоит из учащихся с хорошей подготовкой, которые имеют повышенный интерес к предмету.
В общем, задания 2 и 3 уровня рассчитаны на более сильных учащихся, т.к. в вариантах Б и В преобладают задания комбинированного характера, требующие установления связей между отдельными компонентами курса и применения нестандартных приемов решения.
Дифференцированный подход осуществляется на определенных этапах урока. Так, на этапе изучения нового материала работаю со всем классом, без деления его на группы. Но после того, как несколько упражнений выполнено на доске, учащиеся приступают к дифференцированной самостоятельной работе. Ее особенность состоит не только в том, что учащиеся получают задания различного содержания, но и формой их подачи. Например, на карточке задания всех уровней учащихся самостоятельно выбирают тот или иной вариант.
Следующая форма применения разноуровневых заданий заключается в следующем: все учащиеся начинают свою деятельность с выполнения заданий первого уровня. Пропуск невыполненных заданий не допускается. По мере правильного и последовательного их выполнения переходят на следующие уровни. Это порождает среди учащихся соревновательный момент и гарантирует получение учащимися, «даже не желающими в будущем иметь ничего общего с математикой» знаний на уровне общеобязательного стандарта образования, которые оцениваются в 5 баллов и соответствуют «зачету». Для них считается достаточным регулярное и качественное выполнение всех заданий до второго уровня (включительно) усвоения по каждой теме, при котором снижается общая учебная нагрузка и появляется возможность сэкономить время на достижение более высоких уровней по «любимому» предмету. Вместе с тем, для учащихся, желающих заниматься математикой в соответствии с их способностями и степенью познавательной деятельности создаются условия для перехода на более высокий уровень по данной дисциплине.
Такой подход позволяет решать важную дидактическую задачу — предоставить слабым ученикам возможность решать более простые задания из обязательного уровня обучения и постепенно переходить к выполнению более сложного уровня; сильные учащиеся быстрее проходят начальный этап выполнения заданий 1, 2 уровня, что позволяет большую часть времени уделять заданиям творческого характера.
Также можно в группы объединить учащихся с различным уровнем знаний. Все учащиеся получают карточки с заданиями 1 уровня. Учащиеся, которые первыми правильно выполняют задания, становятся консультантами и проверяют выполнение заданий остальными учащимися. При этом осуществляют консультационную помощь. Затем, аналогично, выполняют задание 2 уровня, далее 3 уровня. Контроль и оценка выполненной работы осуществляется следующим образом: консультантам отметку выставляет учитель, остальных учащихся оценивает консультант. Если кто-то из консультантов затрудняется в оценке знаний одноклассников, то он обращается за помощью к группе и учителю.
Применение разноуровневых заданий дают положительный эффект. Работа по таким заданиям способствует рождению интереса к процессу учения, возникает чувство удовлетворенности не только результатом, но и самим процессом учения.
Таким образом, использование разноуровневых заданий позволяет организовать работу учащихся в соответствии с их возможностями. Разноуровневые задания дают возможность реализовать идеи развивающего обучения, так как они учат мыслить, представлять и запоминать, повышают мотивацию и активность учащихся.
Тема урока:Арифметическая прогрессия
Цели урока:
Образовательная: проверка уровня усвоения теоретических знаний и умения применять их в решении задач.
Развивающая: развитие речи, умения правильно излагать свои мысли, анализировать и делать выводы.
Воспитательная: воспитание интереса к предмету, потребности к знаниям.
Тип урока: урок- зачет
Оборудование урока: карточки трех видов, тесты трех видов.
Ход урока:
I. Мотивационный настрой.
а) приветствие
б) сообщение темы и цели урока
II.Актуализация базовых знаний.
Я буду задавать вопросы, а вы отвечаете, записывая первую букву каждого ответа:
— множество, элементы которого можно пронумеровать (последовательность)
— формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие (рекуррентная)
— угол, градусная мера которого меньше 90 градусов (острый)
— единица измерения углов (градус)
— отрезок, соединяющий точку окружности с его центром (радиус)
— основоположник геометрии (Евклид)
— деление числителя и знаменателя на их общий делитель, отличный от единицы
(сокращение дробей)
— урок на казахском языке (сабақ)
— река, протекающая по нашему району (Ишим)
— числовой промежуток (а, в) (интервал) Какое слово получили? (Прогрессии)
Что означает слово прогрессия? Латинское слово, означающее "движение вперед", было введено римским автором Боэцием (VI в) и понималось в более широком смысле, как бесконечная числовая последовательность.
III. Поясняет правил при выполнении заданий:
Ученики по желанию выбирает одну карточку (любую). Ознакомившись с содержанием выбранной карточки, ученик выполняет задания, либо может эту карточку положить обратно и выбрать другую, но только из другого уровня. Повторно брать карточки одного вида нельзя. Можно выбирать карточки три раза (из каждой группы -по одной соответственно). Ученик, выбравший карточку варианта А получит не выше отметки – 3, варианта Б получит не выше – 4, варианта В может получить — 5.
При отличном ответе на вопросы любого уровня, с согласия учителя, ученик может повысить свою оценку, взяв карточку более сложного уровня. Задания зачета комбинированные. При подготовке ученик имеет право получить один раз краткую консультацию учителя или консультанта.
Тестовые задания для учащихся, работающих по карточкам уровня А:
А- I
1. Найдите 8-й член арифметической прогрессии: 21, 18, 15, …
А. 6. В. 3. С. 0. D. -3.
2. Найдите 12-й член арифметической прогрессии, если а1=7; d=1,5.
А. 17,5. В. 19. С. 20,5. D. 22.
3. Запишите п-й член арифметической прогрессии: 1; 2,5; 4; 5,5; 7; …
А. Зn-1. В. 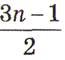
С. 3n-0,5. D. 1,5n-1.
4. Запишите общий член арифметической прогрессии, если а2=3; d=-2.
А. 7-2n. В. 7n-2. С. 3-2n. D. Зn-2.
5. Найдите разность арифметической прогрессии, если а1=3; а5=-1.
А. 2. В. 1. С.-1. D. -2.
А- П
1. Найдите 9-й член арифметической прогрессии: 32, 30, 28; …
А. 22. В. 20. С. 18. D. 16.
2. Найдите 13-й член арифметической прогрессии: а1=8; d=0,5.
А. 15. В. 14. С. 13. D. 12.
3. Запишите общий член арифметической прогрессии, если а3=4; d = -1,5.
А. 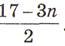
В. 17-Зn. С. 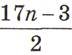
D. 17n-3.
4. Запишите п-й член арифметической прогрессии: 2; 2,3; 2,6; 2,9; …
А. 1,7+0,З n. В. 2+0,3n. С. 0,3n+2. D. 0,З n+1,7.
5. Найдите разность арифметической прогрессии, если а2 = 2; а4= -2.
А. -4. В. -З. С. -2. D. -1.
Тестовые задания для учащихся, работающих по карточкам уровня Б:
Б-I
1. Найдите первый член и разность арифметической прогрессии, если a2+a4= 8, a8 — a3=5.
А. a1 = 4, d= 2. В. a1= 2, d= l.
С. a1= 2, d= — 2. D. a1 = — 2, d = 2.
2. Найдите 7-й член арифметической прогрессии, если a1 + a3 = 8, a5 – a2 =3
А. 6. В. 9. C. 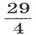
D. 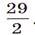
3. Является ли членом арифметической прогрессии an= 5n-3 число: а) 137; б) 108 .
А. а) да; б) да; В. а) нет; б) нет; С. а) да; б) нет; D. иной вариант.
4. Сколько имеется трехзначных натуральных чисел, кратных 11?
А. 78. В. 79. С. 80. D. 81.
5. Какие из последовательностей являются арифметической прогрессией: ап = 3- 4п; 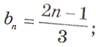
с =3п2 + п?
А. {сп}; В. {сп}, {bп}; С. [ап}, { bп }; D. все три.
Б-П
1. Найдите первый член и разность арифметической прогрессии, если а4+а7=8, а8- аб=6.
А. а1= — 5, d=2. В. а1= -3, d= 2. С. а1=4, d= -2. D. a1=-2, d=1.
2. Найдите 8-й член арифметической прогрессии а2+а6=18, а7-а5=4.
А. 16. В. 17. С. 18. D. 19.
3. Является ли членом арифметической прогрессии аn=7-2n число а) 172; б) .208 .
А. а) да; б) да. В. а) нет; б) нет.
С. а) нет; б) да. D. иной вариант.
4. Сколько имеется трехзначных натуральных чисел, кратных 13?
А. 67. В. 68. С. 69. D. 70.
5. Какие из последовательностей являются арифметической прогрессией: аn= 5 -3n; bn = n2- 4n; 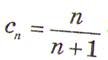 ?
?
А. {аn}; В. Все;
С. {аn},{bn}; D. {bn},{сп} .
Открытые тестовые задания для учащихся, работающих по карточкам уровня В:
B-1
1. Сколько имеется натуральных чисел, меньше 1000, кратных 2 или 7?
2. Положительные члены арифметической прогрессии {an} удовлетворяют равенствам а3 + а4 + а5 + а6 = 64, а3* а6 = 252. Чему равен 10-й член этой прогрессии?
3. Запишите формулу члена последовательности:
а) 7; 13; 25; 49; 97 … б) x1=1, хп+1=3-хп.
B— 2
1. Найти сумму семи первых членов арифметической прогрессии, если а1= -3, d= 7
2. Большее значение х, при котором х+1,4х-1 и х +3 составляют арифметическую прогрессию ?
3. Арифметическая прогрессия, a1+a4+a13= 21, найти а6-?
ЗАДАНИЯ
для карточек уровня А (теоретический тур):
1. Сформулируйте определение арифметической прогрессии. Какое число называют разностью арифметической прогрессии?
2. Запишите формулу n-го члена арифметической прогрессии..
3. Запишите формулу суммы п первых членов арифметической прогрессии
Практические задания уровня А
1.(аn) — арифметическая прогрессия: 19,15. 11………..найти а5
2. Выразить через a1 и d, а7. a23, an
З.(сn)- арифметическая прогрессия . Найти с5 , если с 1=20, d =3.
ЗАДАНИЯ
для карточек уровней Б и В (теоретический тур):
1. Вывести формулу n-го члена арифметической прогрессии.
2. Вывод формулы суммы п первых членов арифметической прогрессии.
Практические задания уровня Б и В
1. Сколько двухзначных чисел делится без остатка на 6, 13?
2. Найти a1 и dарифметической прогрессии, если а5=27,а27=60
3. Если а1=32, d = -1,5, то являются ли числа 0,-28 членами этой арифметической прогрессии?
4. Является ли последовательность (an) арифметической прогрессией? если она задана формулами: аn=Зn+1, аn=n2 -5, аn=-0.5n +1 а6=6n
5. Сколько общих членов имеют арифметические прогрессии: 5,8, 11….и 3,7,11….при n = 100
6. Найдите двадцатый член возрастающей арифметической прогрессии (an), если выполнены равенства а2*а5=52, а2+а3+а4+а5=34
IV. Проверка заданий
1. У доски работают самостоятельно те учащиеся, которые взяли карточки уровня В, их ответы проверяет сам учитель.
2. На местах индивидуально работают учащиеся, взявшие карточки уровня А и Б соответственно.
Если ученик отвечает на отлично по карточке уровня В, то он становится консультантом и помогает учителю принять зачет у учащихся с карточкой уровня А, и с карточкой уровня Б.
V. Итоги урока. Рефлексия. Оценки.
VI. Домашние задание.
№ 193, № 195 стр. 66- 67
Список литературы
Г. Ж. Жадрина. Задания как средство реализации разноуровневой подготовки учащихся.
Г. Ж. Жадрина. Разноуровневые задания как средство достижения планируемых результатов обучения.
М. Б. Миндюк. (Москва) журнал «Математика в школе» №3 1991 г. Составление и использование разноуровневых заданий для дифференцированной работы с учащимися
Шыныбеков А. Н. Алгебра. Сборник дидактических материалов. 9 класс.
А. Абылкасымова, И. Бекбоев, А. Абдиев, З. Жумангулова. Алгебра. Учебник для 9 класса.
