Сумма n первых членов арифметической прогрессии

Тема:  "Сумма  n первых членов арифметической  прогрессии".

Тип урока: Урок изучения нового материала.

Класс: 9Б.

Цели:

 образовательные — познакомить учащихся с выводом формулы сумм n первых членов арифметической прогрессии; научить учащихся применять полученные формулы при решении задач.

развивающие — сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.

воспитательные – трудолюбие, волю, ответственное отношение к учебе.

Ход урока

1. Организационный момент.
2. Проверка домашнего задания.

1. Устный фронтальный опрос:

1. Дайте определение арифметической прогрессии
2. Какое число называется разностью арифметической прогрессии?
3. Составьте арифметическую прогрессию, если ее первый член равен  4
4. Какие из перечисленных последовательностей являются арифметическими прогрессиями?                                

  (an): 0; 1; 8; 27; 64;  …

(bn): 7;  5; 3; 1; -1; …

(xn): 2; 2,2; 2,6; 3,2; 4; …

(cn): 6; 12; 18; 24; 30; …      

2. Задания для индивидуальной работы у доски:

1. Запишите формулу n-ого члена арифметической прогрессии;
2. Запишите формулы 8 и 24 членов арифметической прогрессии;
3. Выразите из предыдущих формул  a1 и d.

III.  Актуализация знаний

Выпишите числа, соответствующие количеству блоков каждого ряда: 19, 17, 15, 13, 11, 9, 7, 5. Получили последовательность чисел. Опишите её.

2. Придумайте арифметическую прогрессию. Кто хочет доказать, что придуманная им последовательность чисел является арифметической  прогрессией.

Каким еще способом можно доказать?

Найдите 20 член этой прогрессии.

1. Обьяснение нового материала

Существует предание о маленьком вундеркинде Карле Гауссе, будущем немецком «короле математики», решившем в 10 летнем возрасте очень быстро задачу о нахождении суммы первых ста натуральных чисел.

1   + 2   + 3   +…+ 98 + 99 + 100 = S.

100 + 99 + 98 +…+ 3   + 2   +  1    = S

101 + 101 + 101 +… + 101 +101 +101 = 2 S;

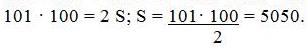
Не помогут ли аналогичные рассуждения нам в достижении нашей цели.

Воспользуйтесь идеей Гаусса  для  решения задачи про плитки.

Задача

Рабочий выложил плитку следующим образом: в первом ряду — 3 плитки, во втором — 5 плиток и т.д., увеличивая каждый ряд на 2 плитки.  Сколько потребуется рабочему плиток, чтобы выложить 6 рядов

Решение:

Составьте  к задаче последовательность из 6 чисел: 3, 5, 7, 9, 11,13

Нетрудно убедиться, что данная последовательность является арифметической прогрессией.

Чтобы узнать количество всех плиток, надо узнать сумму этих чисел, т.е найти сумму первых 6 членов арифметической прогрессии.

Подумайте как найти количество всех плиток

(Ответы учеников)

Д а, можно решить эту задачу непосредственным сложением чисел. Но этот способ не рационален.  А если бы перед вами стояла задача: найти S100, как вы думаете сколько времени вам потребовалось?

Что получилось?

А теперь попробуйте решить эту же задачу, но для 5 рядов.

Можно ли решить эту задачу тем же самым сособом? Почему?

Значит существует другой способ решения данной задачи.

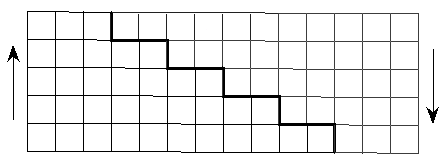
Рис. 1

Сумму 3+5+7+9+11 можно изобразить так, как показано на рис. 1 и из двух таких фигурок составить прямоугольник .Продолжим рассуждения:

S = 3 + 5 + 7 + 9 + 11.

Напишем в обратном порядке:

S = 11 + 9 + 7 + 5 + 3.

И сложим эти равенства:

S = 3 + 5 + 7 + 9 + 11 + + 11 + 9 + 7 + 5 + 3.

В каждом столбце стоят 2 числа, дающие в сумме 14. Поэтому:

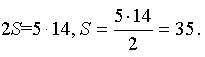
Подтвердим, что применяя этот способ, можно легко найти S100 натуральных чисел. (Самостоятельная работа учащихся)

Во всех задачах мы находили Sn.  Выведем  формулу Sn  для общего случая.

Вывод: в общем случае будет n столбцов с одинаковой суммой, равной сумме первого и последнего членов.

Поэтому

 

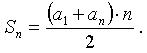
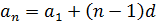,  подставим в формулу, получим: 

 

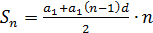
Выполним преобразование:

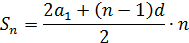
V. Первичное  закрепление

Учитель: математику учить надо за то, что она ум в порядок приводит. Математика миру подарила формулы, которые позволяют делать различные расчеты. Перед нами стоит задача научиться применять формулы суммы n-первых членов арифметической прогрессии.

Учащиеся работают в группах.

1 группа. Задана арифметическая прогрессия (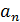), где  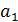=7;  d=2;  n=20. Найти .

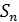2 группа. Задана арифметическая прогрессия (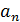), где  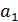=7;  d=2;  n=10. Найти .

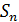3 группа. Задана арифметическая прогрессия (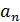), где
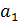 =5;  d=2;  n=12. Найти .

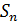Решение упражнений из учебника.  №190а),  № 191

1. Задание на дом: §11, № 185, № 186
2. Итог урока: оценивание учащихся с комментированием.

Учитель: внимательно посмотрите на изученные формулы: которая из них более удобна в применении?

1. Зависит от ситуации задачи.