Трапеция.
Попова. И. Я. учитель математики,
Северо-Казахстанская область, Тайыншинский район,
с. Новодворовка, Новодворовская ОШ
Цель урока:
обучающие:
— организовать самостоятельную деятельность по обобщению и систематизации знаний;
— научить применять свойства трапеции при решении задач;
— научить при формулировке свойств, обращаться к чертежу.
развивающие:
— формирование умений выбирать рациональный способ решения задач;
— применять математические знания в практических ситуациях, описанных условием задач;
— развитие самостоятельной мысли¬тельной деятельности, внимания, точности;
— развитие познавательного интереса к предмету.
воспитывающие:
— воспитание мотивации учения, раскрывая профессиональную значимость изучаемого материала;
— воспитание патриотизма, уважения и чувства гордости к достижениям родной Республики;
— воспитание чувства коллективизма и ответственности.
Тип урока: совершенствование знаний и способов деятельности.
Вид урока: урок математический бой.
Методы обучения: репродуктивный и частично-поисковый.
Ход урока
I. Организационный этап (проверка готовности учащихся к занятию) Приветствие. Организация внимания учащихся.
Психологический тренинг (направленный на создание комфортной обстановки и снятие напряжение учащихся).
— Закройте глаза, представьте, что мы сидим с вами в лесу на поляне где ярко зеленая сочная трава, вздохните три раза ароматами свежести и неприкосновенности нашего леса. Откройте глаза. С хорошим настроением приступим к работе
К сегодняшнему уроку вам, ребя¬та, было задано записать всевозмож¬ные свойства особого вида четырехугольника, как трапеция. Мы с вами договорились на прошлом уроке, что сегодня у нас пройдет математический бой. Между мною, учителем, и вами, учениками, по свойствам трапеции: кто назовет большее количество свойств, тот и выиграет.
Ведь даже обидно за трапецию? Мы так много знаем свойств и даже признаков параллелограмма, а вот о трапеции пока очень мало знаем. А чем, на деле, трапеция хуже параллелограмма?
II. Актуализация субъективного опыта учащихся
Учитель сообщает учащимся условия проведения математического боя:
— Я начинаю первым, формулирую одно из свойств трапеции, а вы — дру-гое, и т.д. Если вы не можете назвать следующее свойство, то опять говорю я. За каждое верно сформулированное свойство дается один балл. Причем, ребята, старайтесь по ходу урока фиксировать свойства в своих тетрадях.
Итак, если всем ясны условия про¬ведения математического боя, то начнем его. Учитель делит доску линией пополам. Слева он будет вести запись свойств, который сформулирует сам, справа — которые назовут ученики, с соответствующими чертежами.
Учитель формулирует первое свойство трапеции:
— Средняя линия трапеции равна полусумме оснований трапеции. (1)
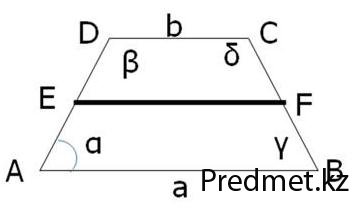
Рис. 1
Ученик формулирует следующее свойство:
— Средняя линия трапеции параллельна основаниям, т.е. EF ІІ АВ, EF ІІ CD (рис. 1) (2)
Учитель:
— Сумма внутренних углов трапеции, прилежащих к боковой стороне равна 1800, т.е.
α + δ =β + γ = 1800 (рис.1). (3)
Ученик продолжает перечень свойств трапеции:
— Если трапеция равнобедренная, то углы при основании равны. (4)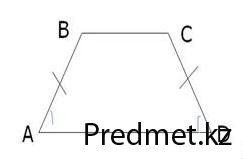
рис. 2.
Если АВ = CD, то ∠ A = ∠ D (рис.2)
Учитель:
— Если соединить середины оснований трапеции отрезком, то этот отрезок будем называть тоже средней линией трапеции. (рис.3).
Итак, средние линии трапеции де¬лаются пересечения пополам.
(рис.3)
ЕСЛИ PQ и EF — средние линии трапеции, которые пересекаются в точке K, то PK = KQ, EK = KF. (5)
Ученик выручает команду школьников:
— Если из вершин трапеции опустить на нижнее основание два перпендикуляра, то длины этих перпендикуляров равны. (6)
Учитель напоминает ребятам, что эти перпендикуляры называются высотами трапеции и что при решении задач нередко проводят именно эти две высоты трапеции, разбивая ее на два прямоугольных треугольника и прямоугольник.
Учитель формулирует:
-Если точки E, P, F, Q – середины сторон трапеции, то четырехугольник EPFQ – параллелограмм 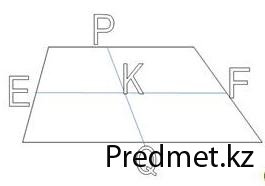
(рис.3) (7)
Ученик называет такое свойство трапеции:
— Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
(рис.4) (8)
(рис.4)
Учитель похвалил ученика и продолжил:
— Точка пересечения боковых сторон и середина оснований трапеции лежат на одной прямой (рис.5). (9)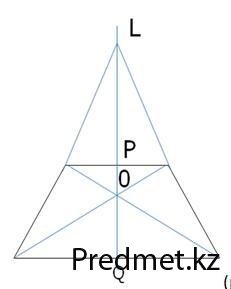
(рис.5)
Ученик сформулировал такое свойство трапеции:
— Середины оснований трапеции и точка пересечения диагоналей трапеции лежат на одной прямой (рис. 5). (10)
Учитель:
— Четыре точки: PQLO лежат на одной прямой, где Р и Q – середины оснований, О — точка пересечения диагоналей, L — точка пересечения боко¬вых сторон трапеции (рис. 5). Это очень, важное свойство. (11)
Ученик продолжил перечень свойств трапеции:
— В равнобедренной трапеции средние линии перпендикулярны. (12)
Учитель:
— В равнобедренной трапеции прямая, проходящая через середины оснований, является осью симметрии. (13)
Ученик продолжил:
— Если в трапеции проведен отрезок с, параллельный основаниям а и b и делящий боковую сторону в отношении p : q, то
(14)
Учитель:
— Если трапеция равнобедренная, то около нее можно описать окружность. (15)
Ученик:
— Если в трапеции ABCD диагонали АС и ВD перпендикулярны, E, F, P, Q – середины сторон трапеции, то EFPQ ромб (рис.3) (16)
Учитель:
— Если АBCD – трапеция, то треугольники DOC и AOB подобны (рис.4) (17)
III. Итоги математического боя.
IV. Решение задач с применением свойств трапеции.
Работа в парах по карточкам. Проверка.
Карточка №1
Меньшее основание трапеции равно 4 см. Большее основание больше средней линии на 4 см. Найти дли¬ну средней линии трапеции.(ответ: 8см) (приложение)
Карточка №2
Средняя линия трапеции равна 9 см, а одно из осно¬ваний равно 6 см. Найти другое основание трапеции. (ответ: 12см) (приложение)
Карточка №3
Боковые стороны и меньшее основание прямоугольной трапеции соответственно равны 8, 10,10. Найти большее основание. (ответ: 16см) (приложение)
Карточка №4
В равнобедренной трапеции основания равны 10 и 24, боковая сторона 25. Найти высоту. (ответ: 24см) (приложение)
Дополнительное задание. Тест.
Высота трапеции 4 см, а углы при большем основании 30 и 45. Найдите боковые стороны. (ответ: В) (Приложение)
А) 45 см и 8 см.
В) 4 см и 8 см.
С) 42 см и 4 см.
D) 45 см и 42 см.
Е) 8 см и 4 см.
V. Рефлексия.
Оказывается, не только параллелограмм, но и трапеция обладает многими свойствами, только нужно суметь их заметить. Но, что особенно ценно, так это то, что теперь мы можем сформулировать и доказать еще и признаки трапеции о которых даже не упоминается в нашем учебнике. И я думаю, что мы не все свойства трапеции назвали сегодня. Так что эту работу вы можете продолжить дома.
VI. Выставление оценок.
VII. Домашние задание.
п.7,§ 3 стр. 13 – 14, № 42 стр.15.
Литература:
1. Симонов А. Я, Бакаев Д. С, Мостовой Р. М и др. Система тренировочных задач и упражнений по математике. : «Просвещение», 1991
2. Асаинов Ж. Сборник тестов: Учебно – методическое пособие. – Астана: Национальный центр государственных стандартов образования и тестирования: Астана- 2005.
Скачать приложение [attachment=200]
