Page 107 - Жоғарғы математика кітабы

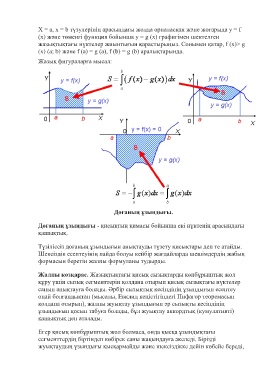
X = a, x = b түзулерінің арасындағы жолда орналасқан және жоғарыда y = f
(x) және төменгі функция бойынша y = g (x) графигімен шектелген
жазықтықтағы нүктелер жиынтығын қарастырыңыз. Сонымен қатар, f (x)> g
(x) (a; b) және f (a) = g (a), f (b) = g (b) аралықтарында.

Жазық фигураларға мысал:

Доғаның ұзындығы.

Доғаның ұзындығы - қисықтың қимасы бойынша екі нүктенің арасындағы
қашықтық.

Түзіліссіз доғаның ұзындығын анықтауды түзету қисықтары деп те атайды.
Шексіздік есептеуінің пайда болуы кейбір жағдайларда шешімдердің жабық
формасын беретін жалпы формуланы тудырды.

Жалпы көзқарас. Жазықтықтағы қисық сызықтарды көпбұрыштық жол
құру үшін сызық сегменттерін қолдана отырып қисық сызықтағы нүктелер
санын анықтауға болады. Әрбір сызықтық кесіндінің ұзындығын есептеу
оңай болғандықтан (мысалы, Евклид кеңістігіндегі Пифагор теоремасын
қолдана отырып), жалпы жуықтау ұзындығын әр сызықты кесіндінің
ұзындығын қосып табуға болады, бұл жуықтау аккордтық (кумулятивті)
қашықтық деп аталады.

Егер қисық көпбұрыштық жол болмаса, онда қысқа ұзындықтағы
сегменттердің біртіндеп көбірек саны жақындауға әкеледі. Бірізді
жуықтаудың ұзындығы қысқармайды және шексіздікке дейін көбейе береді,