Page 49 - Жоғарғы математика кітабы

/
оңға) f (x 0) туындысы плюстен минусқа ауысса, - максимум нүкте,
минустан плюске -минимум нүктесі
Д/уі. нүктесінің маңайын

қарастырайық. және
, шарттары орындалсын делік.

Сонда функциясы интервалында өседі,
ал интервалында кемиді.

Бұдан, функциясының нүктесіндегі
мәні интервалындағы ең үлкен болатындығы шығады, яғни

барлық үшін болады.
Бұл функциясының максимум нүктесі болатындығын білдіреді.

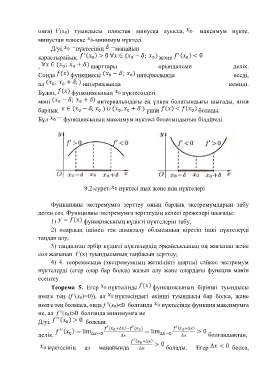
9.2-сурет- нүктесі max және min нүктелері

Функцияны экстремумға зерттеу оның барлық экстремумдарын табу
деген сөз. Функцияны экстремумға зерттеудің келесі ережелері шығады:
1) функциясының күдікті нүктелерін табу;

2) олардың ішінен тек анықталу облысының кіретін ішкі нүктелерді
таңдап алу;
3) таңдалған әрбір күдікті нүктелердің әрқайсысының оң жағынан және
/
сол жағынан f (x) туындысының таңбасын зерттеу;
4) 4. теоремасына (экстремумның жеткілікті шарты) сәйкес экстремум
нүктелерді (егер олар бар болса) жазып алу және олардағы функция мәнін
есептеу.

Теорема 5. Егер нүктесінде функциясының бірінші туындысы
нөлге тең (f (x 0)=0)), ал нүктесіндегі екінші туындысы бар болса, және
/
//
нөлге тең болмаса, онда f (x 0)<0 болғанда нүктесінде функция максимумға
//
ие, ал f (x 0)>0 болғанда минимумға ие
Д/уі. болсын

делік. болғандықтан,

нүктесінің аз маңайында болады. Егер болса,